Research Article
Metrization of Ranked Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-389
-
- Article
-
- You have access
- Export citation
Commutative Systems of Covariance and a Generalization of Mackey's Imprimitivity Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 390-397
-
- Article
-
- You have access
- Export citation
Separating Points and Coloring Principles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 398-404
-
- Article
-
- You have access
- Export citation
Mean Growth of Harmonic Functions of Beurling Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 405-409
-
- Article
-
- You have access
- Export citation
On p-Large Subgroups of p-Torsion Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 410-416
-
- Article
-
- You have access
- Export citation
Generalized Cesàro Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 417-422
-
- Article
-
- You have access
- Export citation
Compactness in Topological Hjelmslev Planes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 423-429
-
- Article
-
- You have access
- Export citation
On Spectral Synthesis and Ergodicity in Spaces of Vector-Valued Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 430-435
-
- Article
-
- You have access
- Export citation
Cubic and Higher Order Algorithms for π
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 436-443
-
- Article
-
- You have access
- Export citation
A Decomposition Theorem for Certain Bipolynomial Hopf Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 444-447
-
- Article
-
- You have access
- Export citation
On Homotopy Domination
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 448-451
-
- Article
-
- You have access
- Export citation
The Almost Lindelöf Degree
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 452-455
-
- Article
-
- You have access
- Export citation
On the Commutativity of a Ring with Identity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 456-460
-
- Article
-
- You have access
- Export citation
Short Proof of an Internal Characterization of Complete Regularity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 461-462
-
- Article
-
- You have access
- Export citation
Inequalities for Entire Functions of Exponential Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 463-471
-
- Article
-
- You have access
- Export citation
On the Monotonic Variation of the Zeros of Ultraspherical Polynomials with the Parameters
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 472-477
-
- Article
-
- You have access
- Export citation
A Brouwer Type Coincidence Theorem and the Fundamental Theorem of Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 478-480
-
- Article
-
- You have access
- Export citation
Tensor Products and Singularly Continuous Spectrum
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-484
-
- Article
-
- You have access
- Export citation
A Finite Index Property of Certain Solvable Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 485-489
-
- Article
-
- You have access
- Export citation
Finite Unions of Quasi-Independent Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 490-493
-
- Article
-
- You have access
- Export citation

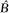 , le complété
, le complété 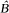 engendrés par un élément.
engendrés par un élément.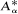 is the operator formally defined on the Hardy space
is the operator formally defined on the Hardy space 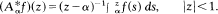
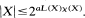
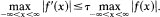
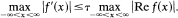
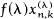 increases with λ, for 0< λ < 1,
increases with λ, for 0< λ < 1, 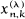 being the kth zero of the ultraspherical polynomial
being the kth zero of the ultraspherical polynomial 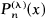 and
and  and an estimate for
and an estimate for 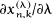 can be obtained.
can be obtained.