Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-24T11:18:40.164Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities for Entire Functions of Exponential Type

Published online by Cambridge University Press:  20 November 2018

Clément Frappier
Clément Frappier*
Affiliation:
Département de Mathématiques et de Statistique, Université de Montréal, C. P. 6128, Succursale “A” Montréal, Québec, H3C 3J7, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Bernstein's inequality says that if f is an entire function of exponential type τ which is bounded on the real axis then

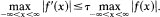
Genchev has proved that if, in addition, hf (π/2) ≤0, where hf is the indicator function of f, then

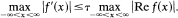
Using a method of approximation due to Lewitan, in a form given by Hörmander, we obtain, to begin, a generalization and a refinement of Genchev's result. Also, we extend to entire functions of exponential type two results first proved for polynomials by Rahman. Finally, we generalize a theorem of Boas concerning trigonometric polynomials vanishing at the origin.

Keywords

30D15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 27 , Issue 4 , 01 December 1984 , pp. 463 - 471
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Ankeny, N. C. and Rivlin, T. J., On a theorem of S. Bernstein, Pacific J. Math. 5, (1955), 849-852.CrossRefGoogle Scholar
2. Bernstein, S. N., Sur Vordre de la meilleure approximation des fonctions continues par les polynömes de degré donné, Mémoire de l'académie Royale de Belgique, vol. 4 (1912), 1-103.Google Scholar
3. Bernstein, S. N., Sur une propriété des fonctions entières, Comptes rendus de l'académie des sciences, Paris, vol. 176 (1923), 1602-1605.Google Scholar
4. Boas, R. P., Entire functions, Acad. Press, New York (1954).Google Scholar
5. Boas, R. P., Inequalities for asymmetric entire functions, Illinois J. Math. 1, (1957), 94-97.CrossRefGoogle Scholar
6. Boas, R. P., Inequalities for polynomials with a prescribed zero, Studies in mathematical analysis and related topics (Essays in Honour of George Pölya), Stanford Univ. Press, Stanford, Calif. (1962), 42-47.Google Scholar
7. De Bruijn, N. G., Inequalities concerning polynomials in the complex domain, Nederl. Akad. Wetensch. Proc. 50, (1947), 1265-1272.Google Scholar
8. Duffin, R. J. and Schaeffer, A. C., Some inequalities concerning functions of exponential type, Bull. Amer. Math. Soc. 43, (1937), 554-556.CrossRefGoogle Scholar
9. Genchev, T. G., Inequalities for asymmetric entire functions of exponential type, Soviet Math. Dokl., vol. 19 (1978), No. 4, 981-985.Google Scholar
10. Giroux, A. and Rahman, Q. I., Inequalities for polynomials with a prescribed zero, Trans. Amer. Math. Soc. 193, (1974), 67-98.CrossRefGoogle Scholar
11. Hörmander, L., Some inequalities for functions of exponential type, Math. Scand. 3, (1955), 21-27.CrossRefGoogle Scholar
12. Lax, P. D., Proof of a conjecture of P. Erdos on the derivative of a polynomial, Bull. Amer. Math. Soc. 50, (1944), 509-513.CrossRefGoogle Scholar
13. Lewitan, B. M. Über eine Verallgemeinerung der Ungleichungen von S. Bernstein und H. Bohr. Doklady Akad. Nauk SSSR 15 (1937), 169-172.Google Scholar
14. Rahman, Q. I., Functions of exponential type, Trans. Amer. Math. Soc. 135, (1969), 295-309.CrossRefGoogle Scholar
15. Szegö, G., Űber einen Satz des Herrn Serge Bernstein, Schr. Königsb. gelehrt. Ges., Vol, 22 (1928), 59-70.Google Scholar