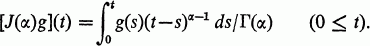Research Article
Contractions with Fixed Points and Conditional Expectation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 475-478
-
- Article
-
- You have access
- Export citation
The Theory of Compositions (I): the Ordered Factorizations of n and a Conjecture of C. Long
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 479-484
-
- Article
-
- You have access
- Export citation
Three Remarks on the Measurement of Unit Spheres
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 485-488
-
- Article
-
- You have access
- Export citation
An N-Parameter Chebyshev Set which is not a Sun
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 489-492
-
- Article
-
- You have access
- Export citation
The Pn-Integral
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 493-497
-
- Article
-
- You have access
- Export citation
Concepts in Vector Spaces with Convergence Structures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 499-502
-
- Article
-
- You have access
- Export citation
Identite Entre L'ensemble Des Fonctions De Baire et L'Ensemble Des Fonctions Boreliennes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 503-506
-
- Article
-
- You have access
- Export citation
A Functional Equation Arising from Ivory's Theorem in Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 507-516
-
- Article
-
- You have access
- Export citation
Analogy in Solving Poisson's Equation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 517-521
-
- Article
-
- You have access
- Export citation
Approximation Polynomiale Generalisee Dans Certains Espaces Semi-Normes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 523-527
-
- Article
-
- You have access
- Export citation
Some Properties of a Certain set of Interpolating Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 529-537
-
- Article
-
- You have access
- Export citation
Morphismes et Multiplications Dans Une Algèbre
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 539-542
-
- Article
-
- You have access
- Export citation
A New Family of Irreducible Representations of An
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 543-546
-
- Article
-
- You have access
- Export citation
Extension of Set Functions to Measures and Applications to Inverse Limit Measures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 547-553
-
- Article
-
- You have access
- Export citation
Weak Convergence and One-Sample Rank Statistics Under ϕ-mixing*
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 555-565
-
- Article
-
- You have access
- Export citation
Isomorphic Group Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 567-576
-
- Article
-
- You have access
- Export citation
On the First Conjugate Point Function for Nonlinear Differential Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 577-585
-
- Article
-
- You have access
- Export citation
Extension Function and Subcategories of Haus
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 587-590
-
- Article
-
- You have access
- Export citation
A Remark on Talenti's Semigroup
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 591-592
-
- Article
-
- You have access
- Export citation
Maximum Modulus Theorems and Schwarz Lemmata for Sequence Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 593-596
-
- Article
-
- You have access
- Export citation

 containing an isolated point.
containing an isolated point.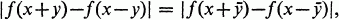
 and
and 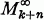 denote the sub-cr-fields generated, respectively, by {X
denote the sub-cr-fields generated, respectively, by {X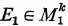 and
and 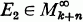 together imply.
together imply.