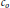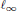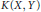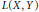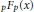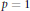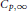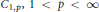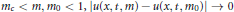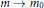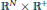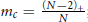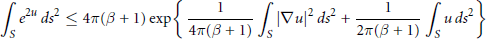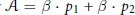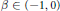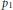Research Article
Complemented Subspaces of Linear Bounded Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-461
-
- Article
-
- You have access
- Export citation
Hook-content Formulae for Symplectic and Orthogonal Tableaux
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 462-473
-
- Article
-
- You have access
- Export citation
A Note on Randers Metrics of Scalar Flag Curvature
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 474-486
-
- Article
-
- You have access
- Export citation
Weighted Model Sets and their Higher Point-Correlations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 487-497
-
- Article
-
- You have access
- Export citation
Simplices in the Euclidean Ball
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 498-508
-
- Article
-
- You have access
- Export citation
Domains of Injective Holomorphy
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 509-522
-
- Article
-
- You have access
- Export citation
The Milnor–Stasheff Filtration on Spaces and Generalized Cyclic Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 523-536
-
- Article
-
- You have access
- Export citation
Asymptotic Properties of Solutions to Semilinear Equations Involving Multiple Critical Exponents
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 537-547
-
- Article
-
- You have access
- Export citation
Non-complemented Spaces of Operators, Vector Measures, and co
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 548-554
-
- Article
-
- You have access
- Export citation
Weighted Lp Boundedness of Pseudodifferential Operators and Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 555-570
-
- Article
-
- You have access
- Export citation
A Generalised Kummer-Type Transformation for the pFp(x) Hypergeometric Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 571-578
-
- Article
-
- You have access
- Export citation
Casimir Operators and Nilpotent Radicals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 579-585
-
- Article
-
- You have access
- Export citation
On Sha's Secondary Chern–Euler Class
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 586-596
-
- Article
-
- You have access
- Export citation
Sharp Inequalities for Differentially Subordinate Harmonic Functions and Martingales
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 597-610
-
- Article
-
- You have access
- Export citation
Chen Inequalities for Submanifolds of Real Space Forms with a Semi-Symmetric Non-Metric Connection
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 611-622
-
- Article
-
- You have access
- Export citation
The Continuous Dependence on the Nonlinearities of Solutions of Fast Diffusion Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 623-631
-
- Article
-
- You have access
- Export citation
Characterizations of Model Manifolds by Means of Certain Differential Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 632-645
-
- Article
-
- You have access
- Export citation
Marcinkiewicz Commutators with Lipschitz Functions in Non-homogeneous Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 646-662
-
- Article
-
- You have access
- Export citation
An Onofri-type Inequality on the Sphere with Two Conical Singularities
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 663-672
-
- Article
-
- You have access
- Export citation