Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-05-09T23:30:34.862Z Has data issue: false hasContentIssue false
  • English
  • Français

An Onofri-type Inequality on the Sphere with Two Conical Singularities

Published online by Cambridge University Press:  20 November 2018

Chunqin Zhou
Chunqin Zhou*
Affiliation:
Department of Mathematics, Shanghai Jiaotong University, Shanghai, 200240, Chinae-mail: cqzhou@sjtu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we give a new proof of the Onofri-type inequality

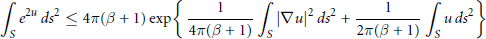$$\int_{S}{{{e}^{2u}}\,d{{s}^{2}}\,\le \,4\pi (\beta \,+\,1)\,\text{exp}}\left\{ \frac{1}{4\pi (\beta \,+\,1)}{{\int_{S}{\left| \nabla u \right|}}^{2}}\,d{{s}^{2}}\,+\,\frac{1}{2\pi (\beta \,+\,1)}\,\int_{S}{u\,d{{s}^{2}}} \right\}$$

on the sphere $S$ with Gaussian curvature 1 and with conical singularities divisor 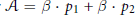$\mathcal{A}\,=\,\beta \,\cdot \,{{p}_{1}}\,+\,\beta \,\cdot \,{{p}_{2}}$ for 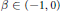$\beta \in \,(-1,\,0)$; here 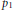${{p}_{1}}$ and 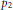${{p}_{2}}$ are antipodal.

Keywords

53C2135J6153A30
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 3 , 01 September 2012 , pp. 663 - 672
Copyright
Copyright © Canadian Mathematical Society 2012

References

[CD1] Chen, W. and Ding, W., A problem concerning the scalar curvature on . Kexue Tongbao 33(1988), 533–537.Google Scholar
[CD2] Chen, W. and Ding, W., Scalar curvatures on . Trans. Amer. Math. Soc. 303(1987), 365–382.Google Scholar
[Ch] Chen, W., A Trudinger inequality on surfaces with conical singularities. Proc. Amer. Math. Soc. 108(1990), 821–832.Google Scholar
[CL] Chen, W. and Li, C., Prescribing Gaussian curvatures on surfaces with conical singularities. J. Geom. Anal. 1991, 359–372.Google Scholar
[CY1] Chang, S. Y. A. and Yang, P., Prescribing Gaussian curvature on . Acta. Math. 159(1987), 215–259. http://dx.doi.org/10.1007/BF02392560 Google Scholar
[CY2] Chang, S. Y. A. and Yang, P., Conformal deformation of metrics on J. Differential Geom. 27(1988), 259–296.Google Scholar
[H] Hong, C., A best constant and the Gaussian curvature. Proc. Amer. Math. Soc. 97(1986), 737–747.Google Scholar
[LZ1] Li, Suyu and Zhu, Meijun, A sharp inequality and its applications. Preprint. http://dx.doi.org/10.1142/S0219199709003430 Google Scholar
[LZ2] Li, Junfang and Zhu, Meijun, Sharp local embedding inequalities. Comm. Pure Appl. Math. 59(2006), 122–144. http://dx.doi.org/10.1002/cpa.20107 Google Scholar
[M] Moser, J., A sharp form of an inequality by Neil Trudinger. Indiana Univ. Math. J. 20(1971), 1077–1092. http://dx.doi.org/10.1512/iumj.1971.20.20101 Google Scholar
[On] Onofri, E., On the positivity of the effective action in a theory of random surface. Comm. Math. Phys. 86(1982), 321–326. http://dx.doi.org/10.1007/BF01212171 Google Scholar
[T1] Troyanov, M., Metrics of constant curvature on a sphere with two conical singularities. Differential Geometry (Peniscola, 1988), Lecture Notes in Math. 1410, Springer-Verlag, Berlin, 1989, 296–308.Google Scholar
[T2] Troyanov, M., Prescribing curvature on compact surfaces with conical singularities. Trans. Amer. Math. Soc. 324(1991), 793–821. http://dx.doi.org/10.2307/2001742 Google Scholar