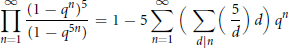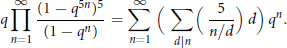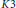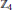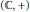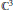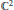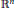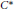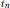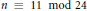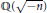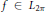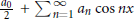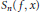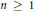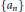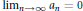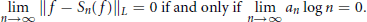Research Article
Some Infinite Products of Ramanujan Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-492
-
- Article
-
- You have access
- Export citation
A One-Dimensional Family of K3 Surfaces with a ℤ4 Action
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 493-510
-
- Article
-
- You have access
- Export citation
The Irreducibility of Polynomials That Have One Large Coefficient and Take a Prime Value
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 511-520
-
- Article
-
- You have access
- Export citation
The Parabolic Littlewood–Paley Operator with Hardy Space Kernels
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 521-534
-
- Article
-
- You have access
- Export citation
A Note on Locally Nilpotent Derivations and Variables of k[X, Y, Z]
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 535-543
-
- Article
-
- You have access
- Export citation
Intuitionistic Fuzzy γ-Continuity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 544-554
-
- Article
-
- You have access
- Export citation
Boundary Behavior of Solutions of the Helmholtz Equation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 555-563
-
- Article
-
- You have access
- Export citation
Group Actions on Quasi-Baer Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 564-582
-
- Article
-
- You have access
- Export citation
Computing Polynomials of the Ramanujan tn Class Invariants
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 583-597
-
- Article
-
- You have access
- Export citation
Numerical Semigroups That Are Not Intersections of d-Squashed Semigroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 598-612
-
- Article
-
- You have access
- Export citation
Lipschitz Type Characterizations for Bergman Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 613-626
-
- Article
-
- You have access
- Export citation
On L1-Convergence of Fourier Series under the MVBV Condition
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 627-636
-
- Article
-
- You have access
- Export citation