Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Daigle, Daniel
2010.
Triangular derivations of k[X,Y,Z].
Journal of Pure and Applied Algebra,
Vol. 214,
Issue. 7,
p.
1173.
El Kahoui, M’hammed
2013.
On residual coordinates and stable coordinates of R [3].
Archiv der Mathematik,
Vol. 100,
Issue. 1,
p.
35.
Dubouloz, Adrien
Finston, David
and
Jaradat, Imad
2014.
Proper triangular 𝔾a-actions on 𝔸4are translations.
Algebra & Number Theory,
Vol. 8,
Issue. 8,
p.
1959.
Stampfli, Immanuel
2015.
Automorphisms of ℂ3Commuting with a ℂ+-Action.
International Mathematics Research Notices,
Vol. 2015,
Issue. 19,
p.
9832.
Dutta, Amartya K.
and
Gupta, Neena
2015.
The epimorphism theorem and its generalizations.
Journal of Algebra and Its Applications,
Vol. 14,
Issue. 09,
p.
1540010.
Freudenburg, Gene
2017.
Algebraic Theory of Locally Nilpotent Derivations.
Vol. 136.3,
Issue. ,
p.
137.
Kaliman, Shulim
2018.
Proper Ga-actions on ℂ4 preserving a
coordinate.
Algebra & Number Theory,
Vol. 12,
Issue. 2,
p.
227.
Dubouloz, Adrien
Pauli, Sabrina
and
Østvær, Paul Arne
2019.
𝔸1-contractibility of affine modifications.
International Journal of Mathematics,
Vol. 30,
Issue. 14,
p.
1950069.
FREUDENBURG, GENE
2019.
CANONICAL FACTORIZATION OF THE QUOTIENT MORPHISM FOR AN AFFINE
G
$$ \mathbb{G} $$
a-VARIETY.
Transformation Groups,
Vol. 24,
Issue. 2,
p.
355.
Daigle, Daniel
2020.
Locally nilpotent derivations and the structure of rings.
Journal of Pure and Applied Algebra,
Vol. 224,
Issue. 4,
p.
106201.
DUTTA, AMARTYA KUMAR
GUPTA, NEENA
and
LAHIRI, ANIMESH
2020.
ON SEPARABLE AND -FORMS.
Nagoya Mathematical Journal,
Vol. 239,
Issue. ,
p.
346.
El Kahoui, M’hammed
Essamaoui, Najoua
and
Ouali, Mustapha
2020.
Interpolation in the Automorphism Group of a Polynomial Ring.
Algebra Colloquium,
Vol. 27,
Issue. 03,
p.
587.
Gurjar, Rajendra V.
Masuda, Kayo
and
Miyanishi, Masayoshi
2020.
Polynomial Rings and Affine Algebraic Geometry.
Vol. 319,
Issue. ,
p.
151.
Pan, Ivan
2022.
A characterization of local nilpotence for dimension two polynomial derivations.
Communications in Algebra,
Vol. 50,
Issue. 5,
p.
1884.
Masuda, Kayo
2023.
Factorial Affine $$G_a$$-Varieties with Height One Plinth Ideals.
Transformation Groups,
Freudenburg, Gene
2024.
Actions of SL2(k) on Affine k-Domains and Fundamental Pairs.
Transformation Groups,
Vol. 29,
Issue. 3,
p.
959.
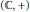 $\left( \mathbb{C},\,+ \right)$ on
$\left( \mathbb{C},\,+ \right)$ on 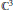 ${{\mathbb{C}}^{3}}$ and embeddings of
${{\mathbb{C}}^{3}}$ and embeddings of 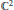 ${{\mathbb{C}}^{2}}$ in
${{\mathbb{C}}^{2}}$ in 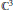 ${{\mathbb{C}}^{3}}$, and show that these results are in fact valid over any field of characteristic zero.
${{\mathbb{C}}^{3}}$, and show that these results are in fact valid over any field of characteristic zero.

