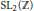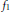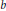Research Article
ZL-amenability Constants of Finite Groups with Two Character Degrees
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-462
-
- Article
-
- You have access
- Export citation
Constructive Proof of the Carpenter's Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 463-476
-
- Article
-
- You have access
- Export citation
On Set Theoretically and Cohomologically Complete Intersection Ideals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 477-484
-
- Article
-
- You have access
- Export citation
Fourier Coefficients of Vector-valued Modular Forms of Dimension 2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 485-494
-
- Article
-
- You have access
- Export citation
Jeśmanowicz’ Conjecture with Congruence Relations. II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 495-505
-
- Article
-
- You have access
- Export citation
On Braided and Ribbon Unitary Fusion Categories
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 506-510
-
- Article
-
- You have access
- Export citation
Simplicity of Partial Skew Group Rings of Abelian Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 511-519
-
- Article
-
- You have access
- Export citation
Maximizing the Index of Trees with Given Domination Number
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 520-525
-
- Article
-
- You have access
- Export citation
On 3-manifolds with Torus or Klein Bottle Category Two
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 526-537
-
- Article
-
- You have access
- Export citation
Infinite Families of A4-Sextic Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 538-545
-
- Article
-
- You have access
- Export citation
Compact Operators in Regular LCQ Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 546-550
-
- Article
-
- You have access
- Export citation
Asymptotic Improvements of Lower Bounds for the Least Common Multiples of Arithmetic Progressions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 551-561
-
- Article
-
- You have access
- Export citation
Note on the Grothendieck Group of Subspaces of Rational Functions and Shokurov's Cartier b-divisors
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 562-572
-
- Article
-
- You have access
- Export citation
Some Results on the Domination Number of a Zero-divisor Graph
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 573-578
-
- Article
-
- You have access
- Export citation
On the Hereditary Paracompactness of Locally Compact, Hereditarily Normal Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 579-584
-
- Article
-
- You have access
- Export citation
Short Probabilistic Proof of the Brascamp-Lieb and Barthe Theorems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 585-597
-
- Article
-
- You have access
- Export citation
Interpolation of Morrey Spaces on Metric Measure Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 598-608
-
- Article
-
- You have access
- Export citation
Jacobson Radicals of Skew Polynomial Rings of Derivation Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 609-613
-
- Article
-
- You have access
- Export citation
A Note on the Weierstrass Preparation Theorem in Quasianalytic Local Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 614-620
-
- Article
-
- You have access
- Export citation
Combinatorially Factorizable Cryptic Inverse Semigroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 621-630
-
- Article
-
- You have access
- Export citation