Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-23T20:24:24.502Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Distribution of Irreducible Trinomials

Published online by Cambridge University Press:  20 November 2018

Igor E. Shparlinski
Igor E. Shparlinski*
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australiae-mail: igor@ics.mq.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We obtain new results about the number of trinomials 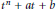${{t}^{n}}\,+\,at\,+\,b$ with integer coefficients in a box 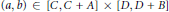$(a,\,b)\,\in \,[C,\,C\,+\,A]\,\times \,[D,\,D\,+\,B]$ that are irreducible modulo a prime 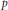$p$. As a by-product we show that for any 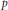$p$ there are irreducible polynomials of height at most 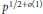${{p}^{1/2+o(1)}}$, improving on the previous estimate of 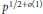${{p}^{2/3+o(1)}}$ obtained by the author in 1989.

Keywords

11L4011T06irreducible trinomialscharacter sums
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 4 , 01 December 2011 , pp. 748 - 756
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Adleman, L. M. and Lenstra, H. W., Finding irreducible polynomials over finite fields. In: Proc. 18th ACM Symp. Theory Comput. (Berkeley, 1986), ACM, New York, 1986, 350–355.Google Scholar
[2] Ayyad, A., Cochrane, T. and Zheng, Z., The congruence x 1 x 2 ≡ x 3 x 4 (mod p), the equation x 1 x 2 = x 3 x 4 and the mean value of character sums. J. Number Theory 59(1996), 398–413. doi:10.1006/jnth.1996.0105Google Scholar
[3] Banks, W. D. and Shparlinski, I. E., Sato–Tate, cyclicity, and divisibility statistics on average for elliptic curves of small height.. Israel J. Math. 173(2009), 253–277. doi:10.1007/s11856-009-0091-0Google Scholar
[4] Cohen, S. D., The distribution of polynomials over finite fields.. Acta Arith. 17(1970), 255–271.Google Scholar
[5] Cohen, S. D., Uniform distribution of polynomials over finite fields.. J. London Math. Soc. 6(1972), 93–102. doi:10.1112/jlms/s2-6.1.93Google Scholar
[6] Friedlander, J. B. and Iwaniec, H., The divisor problem for arithmetic progressions.. Acta Arith. 45(1985), 273–277.Google Scholar
[7] Iwaniec, H. and Kowalski, E., Analytic number theory. Amer. Math. Soc., Providence, RI, 2004.Google Scholar
[8] Shparlinski, I. E., Distribution of primitive and irreducible polynomials modulo a prime.. (Russian) Diskret. Mat. 1(1989), 117–124; translation in Discrete Math. Appl. 1(1991), 59–67.Google Scholar
[9] Shparlinski, I. E., On irreducible polynomials of small height in finite fields. Appl. Algebra Engrg. Comm. Comput. 4(1996), no. 6, 427–431. doi:10.1007/s002000050043Google Scholar
[10] Shparlinski, I. E., Finite fields: Theory and computation. Kluwer Acad. Publ., Dordrecht, 1999.Google Scholar