Article contents
On a Theorem of Kawamoto on Normal Bases of Rings of Integers, II
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 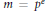 $m={{p}^{e}}$ be a power of a prime number
$m={{p}^{e}}$ be a power of a prime number 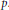 $p$. We say that a number field
$p$. We say that a number field 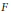 $F$ satisfies the property
$F$ satisfies the property 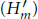 $\left( {{H}^{'}}_{m} \right)$ when for any
$\left( {{H}^{'}}_{m} \right)$ when for any 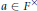 $a\in {{F}^{\times }}$, the cyclic extension
$a\in {{F}^{\times }}$, the cyclic extension 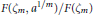 $F\left( {{\zeta }_{m}},{{a}^{1/m}} \right)/F\left( {{\zeta }_{m}} \right)$ has a normal
$F\left( {{\zeta }_{m}},{{a}^{1/m}} \right)/F\left( {{\zeta }_{m}} \right)$ has a normal  $p$-integral basis. We prove that
$p$-integral basis. We prove that 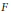 $F$ satisfies
$F$ satisfies 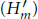 $\left( {{H}^{'}}_{m} \right)$ if and only if the natural homomorphism
$\left( {{H}^{'}}_{m} \right)$ if and only if the natural homomorphism 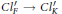 $C{{l}^{'}}_{F}\to C{{l}^{'}}_{K}$ is trivial. Here
$C{{l}^{'}}_{F}\to C{{l}^{'}}_{K}$ is trivial. Here 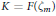 $K=F\left( {{\zeta }_{m}} \right)$, and
$K=F\left( {{\zeta }_{m}} \right)$, and 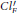 $C{{l}^{'}}_{F}$ denotes the ideal class group of
$C{{l}^{'}}_{F}$ denotes the ideal class group of 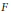 $F$ with respect to the
$F$ with respect to the 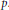 $p$-integer ring of
$p$-integer ring of 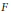 $F$.
$F$.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2005
References
- 2
- Cited by




