Hostname: page-component-848d4c4894-xfwgj Total loading time: 0 Render date: 2024-06-30T05:12:46.613Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of the Continuous q-Ultraspherical Polynomials

Published online by Cambridge University Press:  20 November 2018

Waleed Al-Salam ,
WM. R. Allaway  and
Richard Askey
Waleed Al-Salam
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, CanadaT6G2G1.
WM. R. Allaway
Affiliation:
Department of Mathematical Sciences, Lakehead University, Thunder Bay, Ontario, CanadaP7B5E1.
Richard Askey
Affiliation:
Department of Mathematics, Van Vleck Hall, University of Wisconsin, 480 Lincoln Drive, Madison, Wisconsin, U.S.A.53706.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In his Ph.D. thesis Allaway found all polynomials 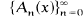that can be represented as

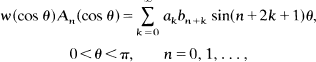
and a0bn≠0. We solve the essentially equivalent problem of finding all symmetric polynomials 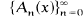with 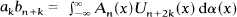when 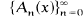are orthogonal with respect to dα(x). The polynomials are the continuous q-ultraspherical polynomials and some of their limiting cases.

Keywords

33A6542A52
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 27 , Issue 3 , 01 September 1984 , pp. 329 - 336
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Al-Salam, W., Allaway, W. R. and Askey, R., Sieved ultraspherical polynomials, Trans. Amer. Math. Soc to appear.Google Scholar
2. Allaway, W. R., The identification of a class of orthogonal polynomial sets, Ph.D. Thesis, University of Alberta, Edmonton, Alberta, Canada, 1972.Google Scholar
3. Askey, R. and Ismail, M., The Rogers q-ultraspherical polynomials, Approximation Theory, III, ed. Cheney, E. W., Academic Press, New York, 1980, 175–182.Google Scholar
4. Askey, R. and Ismail, M., A generalization of ultraspherical polynomials, Studies in Pure Mathematics, ed. P. Erdôs, Birkhàuser, 1983, 55–78.Google Scholar
5. Askey, R. and Ismail, M., Recurrence relations, continued fractions and orthogonal polynomials, Mem. Amer. Math. Soc. to appear.Google Scholar
6. Askey, R. and Wilson, J., Some basic hypergeometric orthogonal polynomials that generalize Jacobi polynomials, Mem. Amer. Math. Soc, to appear.Google Scholar
7. Chihara, T. S., Introduction to Orthogonal Polynomials, (Gordon and Beach, New York, 1978).Google Scholar
8. Rogers, L. J., Third memoir on the expansion of certain infinite products, Proc. London Math. Soc, 26 (1985), 15–32.Google Scholar
9. Szegö, G., Über gewisse orthogonale Polynôme, die zu einer oszillierenden Belegungsfunktion gehoren, Math. Ann. 110 (1934), 501–513. Reprinted, G. Szego, Collected Papers, Vol. 2, Birkhàuser-Boston, 1982, 545–557.Google Scholar
10. Szegö, G., Orthogonal Polynomials, fourth edition, (Amer. Math. Soc, Providence, R.I., 1975).Google Scholar