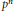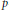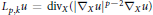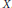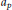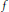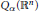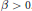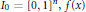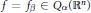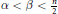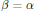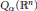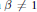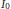Research Article
Multiplicative Isometries and Isometric Zero-Divisors
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-974
-
- Article
-
- You have access
- Export citation
Revisiting Tietze–Nakajima: Local and Global Convexity for Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 975-993
-
- Article
-
- You have access
- Export citation
Curvature Bounds for Surfaces in Hyperbolic 3-Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 994-1010
-
- Article
-
- You have access
- Export citation
Functoriality of the Canonical Fractional Galois Ideal
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1011-1036
-
- Article
-
- You have access
- Export citation
Riemann Extensions of Torsion-Free Connections with Degenerate Ricci Tensor
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1037-1057
-
- Article
-
- You have access
- Export citation
On a Conjecture of S. Stahl
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1058-1059
-
- Article
-
- You have access
- Export citation
Heegner Points over Towers of Kummer Extensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1060-1081
-
- Article
-
- You have access
- Export citation
The Fundamental Group of S1-manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1082-1098
-
- Article
-
- You have access
- Export citation
Character Sums to Smooth Moduli are Small
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1099-1115
-
- Article
-
- You have access
- Export citation
Degenerate p-Laplacian Operators and Hardy Type Inequalities on H-Type Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1116-1130
-
- Article
-
- You have access
- Export citation
Moduli Spaces of Reflexive Sheaves of Rank 2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1131-1154
-
- Article
-
- You have access
- Export citation
Moments of the Critical Values of Families of Elliptic Curves, with Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1155-1181
-
- Article
-
- You have access
- Export citation
A Fractal Function Related to the John–Nirenberg Inequality for Qα(ℝn)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1182-1200
-
- Article
-
- You have access
- Export citation