Research Article
Sets on which Measurable Functions are Determined by their Range
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1089-1116
-
- Article
-
- You have access
- Export citation
The Von Neumann Algebra VN(G) of a Locally Compact Group and Quotients of Its Subspaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1117-1138
-
- Article
-
- You have access
- Export citation
Majorations Effectives Pour L’ Équation de Fermat Généralisée
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1139-1161
-
- Article
-
- You have access
- Export citation
Isoperimetric Inequalities on Surfaces of Constant Curvature
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1162-1187
-
- Article
-
- You have access
- Export citation
Factorization in the Invertible Group of a C*-Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1188-1205
-
- Article
-
- You have access
- Export citation
Subalgebras Which Appear in Quantum Iwasawa Decompositions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1206-1223
-
- Article
-
- You have access
- Export citation
Tensor Products of Analytic Continuations of Holomorphic Discrete Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1224-1241
-
- Article
-
- You have access
- Export citation
1-Complemented Subspaces of Spaces With 1-Unconditional Bases
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1242-1264
-
- Article
-
- You have access
- Export citation
Hecke Algebras and Class-Group Invariants
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1265-1280
-
- Article
-
- You have access
- Export citation
Pieri’S Formula Via Explicit Rational Equivalence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1281-1298
-
- Article
-
- You have access
- Export citation
The Explicit Solution of the
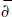 -Neumann Problem in a Non-Isotropic Siegel Domain
-Neumann Problem in a Non-Isotropic Siegel Domain
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1299-1322
-
- Article
-
- You have access
- Export citation
Stable Parallelizability of Partially Oriented Flag Manifolds II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1323-1339
-
- Article
-
- You have access
- Export citation
Other
Author Index for Volume 49, 1997
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1340-1344
-
- Article
-
- You have access
- Export citation

 of
of 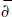 -Neumann Problem in a Non-Isotropic Siegel Domain
-Neumann Problem in a Non-Isotropic Siegel Domain