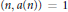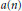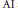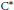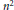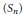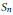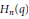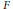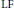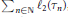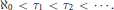Research Article
Multiple Zeta-Functions Associated with Linear Recurrence Sequences and the Vectorial Sum Formula
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-276
-
- Article
-
- You have access
- Export citation
Locally Indecomposable Galois Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 277-297
-
- Article
-
- You have access
- Export citation
A Variant of Lehmer’s Conjecture, II: The CM-case
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 298-326
-
- Article
-
- You have access
- Export citation
Discrete Series for p-adic SO(2n) and Restrictions of Representations of O(2n)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 327-380
-
- Article
-
- You have access
- Export citation
A Complete Classification of AI Algebras with the Ideal Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 381-412
-
- Article
-
- You have access
- Export citation
Generating Functions for Hecke Algebra Characters
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 413-435
-
- Article
-
- You have access
- Export citation
Simplicial Complexes and Open Subsets of Non-Separable LF-Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 436-459
-
- Article
-
- You have access
- Export citation
Monotonically Controlled Mappings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 460-480
-
- Article
-
- You have access
- Export citation