Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-07-05T12:17:23.635Z Has data issue: false hasContentIssue false
  • English
  • Français

A Variant of Lehmer’s Conjecture, II: The CM-case

Published online by Cambridge University Press:  20 November 2018

Sanoli Gun  and
V. Kumar Murty
Sanoli Gun
Affiliation:
The Institute of Mathematical Sciences, CIT Campus, Taramani, India email: sanoli@imsc.res.in
V. Kumar Murty
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON, M5S 2E4 email: murty@math.toronto.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 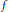$f$ be a normalized Hecke eigenform with rational integer Fourier coefficients. It is an interesting question to know how often an integer 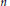$n$ has a factor common with the 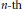$n\text{-th}$ Fourier coefficient of 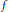$f$. It has been shown in previous papers that this happens very often. In this paper, we give an asymptotic formula for the number of integers 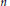$n$ for which 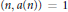$\left( n,\,a\left( n \right) \right)\,=\,1$, where 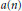$a\left( n \right)$ is the 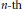$n\text{-th}$ Fourier coefficient of a normalized Hecke eigenform 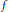$f$ of weight 2 with rational integer Fourier coefficients and having complex multiplication.

Keywords

11F1111F30
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 2 , 01 April 2011 , pp. 298 - 326
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] P., Erdös, Some asymptotic formulas in number theory. J. Indian Math. Soc. 12(1948), 75–78.Google Scholar
[2] Lang, S., Elliptic functions. Addison-Wesley, Reading, MA, 1973.Google Scholar
[3] Lehmer, D. H., Ramanujan's function . (n). Duke Math. J. 10(1943), 483–492. doi:10.1215/S0012-7094-43-01041-5Google Scholar
[4] Lehmer, D. H., The vanishing of Ramanujan's function . (n). Duke Math. J. 14(1947), 429–433. doi:10.1215/S0012-7094-47-01436-1Google Scholar
[5] Murty, M. R. and Murty, V. K., Some results in number theory. I. Acta Arith. 35(1979), no. 4, 367–371.Google Scholar
[6] Murty, M. R. and Murty, V. K., Odd values of Fourier coefficients of certain modular forms. Int. J. Number Theory 3(2007), no. 3, 455–470. doi:10.1142/S1793042107001036Google Scholar
[7] Murty, V. K., Lacunarity of modular forms. J. Indian Math. Soc. 52(1987), 127–146.Google Scholar
[8] Murty, V. K., Modular forms and the Chebotarev density theorem. II. In: Analytic number theory (Kyoto, 1996), London Math. Soc. Lecture Note Ser., 247, Cambridge University Press, Cambridge, 1997, pp. 287–308.Google Scholar
[9] Murty, V. K., Some results in number theory. II. In: Number theory, Ramanujan Math. Soc. Lect. Notes Ser., 1, Ramanujan Math. Soc., Mysorem, 2005, pp. 51–55.Google Scholar
[10] Murty, V. K., A variant of Lehmer's conjecture. J. Number Theory 123(2007), no. 1, 80–91. doi:10.1016/j.jnt.2006.06.004Google Scholar
[11] Ramanujan, S., On certain arithmetical functions. Trans. Cambridge Philos. Soc. 22(1916), no. 9, 159–184. In: Collected papers of Srinivasa Ramanujan, AMS Chelsea, Providence, RI, 2000, pp. 136–162.Google Scholar
[12] Rosen, M., A generalization of Mertens’ theorem. J. Ramanujan Math. Soc. 14(1999), no. 1, 1–19.Google Scholar
[13] Schaal, W., On the large sieve method in algebraic number fields. J. Number Theory 2(1970), 249–270. doi:10.1016/0022-314X(70)90052-1Google Scholar
[14] Serre, J.-P., Divisibilité de certaines fonctions arithmétiques. Enseignement Math. 22(1976), no. 3–4, 227–260.Google Scholar
[15] Serre, J.-P., Quelques applications du théorème de densité de Chebotarev. Inst. Hautes Études Sci. Publ. Math. 54(1981), 323–401.Google Scholar
[16] Serre, J.-P., Sur la lacunarité des puissances de. Glasgow Math. J. 27(1985), 203–221. doi:10.1017/S0017089500006194Google Scholar
[17] Stark, H. M., Some effective cases of the Brauer-Siegel theorem. Invent. Math. 23(1974), 135–152. doi:10.1007/BF01405166Google Scholar