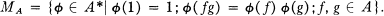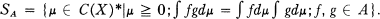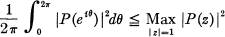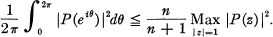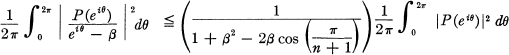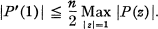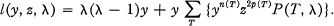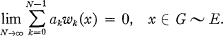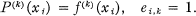Research Article
The Application of Lagrangian Methods to the Enumeration of Labelled Trees with Respect to Edge Partition
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 513-518
-
- Article
-
- You have access
- Export citation
A Polynomial Algorithm for Constructing a Large Bipartite Subgraph, with an Application to a Satisfiability Problem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 519-524
-
- Article
-
- You have access
- Export citation
Three Topological Properties from Noetherian Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 525-534
-
- Article
-
- You have access
- Export citation
Some Finiteness Conditions for Orthomodular Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 535-549
-
- Article
-
- You have access
- Export citation
Real Flexible Division Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 550-588
-
- Article
-
- You have access
- Export citation
Bounds on Betti Numbers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 589-592
-
- Article
-
- You have access
- Export citation
Resolution D'Equations Associees a un Systeme de Tchebycheff
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 593-620
-
- Article
-
- You have access
- Export citation
The Generalized Orthocompletion and Strongly Projectable Hull of a Lattice Ordered Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 621-661
-
- Article
-
- You have access
- Export citation
A Class of Loops Which are Isomorphic to all Loop Isotopes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 662-672
-
- Article
-
- You have access
- Export citation
The Measure Spectrum of a Uniform Algebra and Subharmonicity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-685
-
- Article
-
- You have access
- Export citation
A Stickelberger Condition on Cyclic Galois Extensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 686-690
-
- Article
-
- You have access
- Export citation
Semi-Prime Rings Whose Homomorphic Images are Serial
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 691-695
-
- Article
-
- You have access
- Export citation
Orthomodular Lattices Which can be Covered by Finitely Many Blocks
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 696-699
-
- Article
-
- You have access
- Export citation
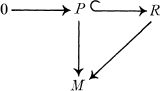
Homology Operations Revisited
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 700-717
-
- Article
-
- You have access
- Export citation
The Associated Ultraspherical Polynomials and their q-Analogues
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 718-736
-
- Article
-
- You have access
- Export citation
Inequalities for Polynomials with a Prescribed Zero
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 737-740
-
- Article
-
- You have access
- Export citation
Chromatic Solutions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 741-758
-
- Article
-
- You have access
- Export citation
Perfect Sets of Uniqueness on the Group 2ω
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 759-764
-
- Article
-
- You have access
- Export citation
The Analytic Character of the Birkhoff Interpolation Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 765-768
-
- Article
-
- You have access
- Export citation



 and for
and for 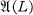 the set of all maximal Boolean subalgebras, also called blocks [
the set of all maximal Boolean subalgebras, also called blocks [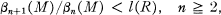
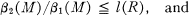
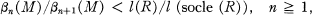
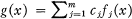 admet au plus
admet au plus  de
de 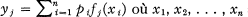 sont
sont