Research Article
The Maximum Genus of Cartesian Products of Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1025-1035
-
- Article
-
- You have access
- Export citation
Algebraically Closed Regular Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1036-1049
-
- Article
-
- You have access
- Export citation
The Translational Hull of an Inverse Semigroup
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1050-1068
-
- Article
-
- You have access
- Export citation
Localization of Right Noetherian Rings at Semiprime Ideals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1069-1085
-
- Article
-
- You have access
- Export citation
The Type I Part of the Regular Representation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1086-1089
-
- Article
-
- You have access
- Export citation
On The Number of Classes of a Finite Group Invariant for Certain Substitutions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1090-1097
-
- Article
-
- You have access
- Export citation
Homomorphisms of Rings with Involution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1098-1108
-
- Article
-
- You have access
- Export citation
A Generalization of the Mapping Degree
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1109-1117
-
- Article
-
- You have access
- Export citation
Irreducible Representations of Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1118-1129
-
- Article
-
- You have access
- Export citation
Pseudodifferential Resolvent for a Certain Non-Locally-Solvable Operator
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1130-1140
-
- Article
-
- You have access
- Export citation
The Structure of Quasi-Frobenius Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1141-1151
-
- Article
-
- You have access
- Export citation
Some Results on Weak Covering Conditions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1152-1156
-
- Article
-
- You have access
- Export citation
The Additive Group of an f-ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1157-1168
-
- Article
-
- You have access
- Export citation
Capacity Estimates for Planar Cantor-Like Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1169-1172
-
- Article
-
- You have access
- Export citation
Quasi-Injective and Quasi-Projective Modules Over Hereditary Noetherian Prime Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1173-1185
-
- Article
-
- You have access
- Export citation
Right Invariant Right Hereditary Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1186-1191
-
- Article
-
- You have access
- Export citation
A Class of Almost Commutative Nilalgebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1192-1198
-
- Article
-
- You have access
- Export citation
Le Spectre des Opérateurs de Composition Sur C[0,1]
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1199-1205
-
- Article
-
- You have access
- Export citation
A Local Ergodic Theorem on Lp
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1206-1216
-
- Article
-
- You have access
- Export citation
Structure Species and Constructive Functors
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1217-1227
-
- Article
-
- You have access
- Export citation

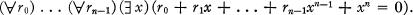
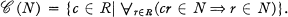

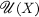 of a (not necessarily associative) algebra
of a (not necessarily associative) algebra 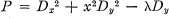 by the method of [3] and study the dependence on the parameter
by the method of [3] and study the dependence on the parameter 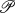 (S) of polar preserving endomorphisms of the
(S) of polar preserving endomorphisms of the 
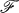 ,
, 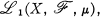 , defined for
, defined for