Research Article
Notes on Extensions of Hopf Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-42
-
- Article
-
- You have access
- Export citation
q-Hermite Polynomials and Classical Orthogonal Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 43-63
-
- Article
-
- You have access
- Export citation
Metrics of Positive Scalar Curvature on Spherical Space Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 64-80
-
- Article
-
- You have access
- Export citation
On the Distribution of Supersingular Primes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 81-104
-
- Article
-
- You have access
- Export citation
On a Generalization of a Result of Waldspurger
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 105-142
-
- Article
-
- You have access
- Export citation
Solvability of Some Singular Boundary Value Problems on the Semi-Infinite Interval
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 143-158
-
- Article
-
- You have access
- Export citation
Moore Cohomology and Central Twisted Crossed Product C*-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 159-174
-
- Article
-
- You have access
- Export citation
C*-Algebras from Smale Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 175-195
-
- Article
-
- You have access
- Export citation
Positive Powers of Positive Positive Definite Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 196-209
-
- Article
-
- You have access
- Export citation
Compact Almost Discrete Hypergroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 210-224
-
- Article
-
- You have access
- Export citation


 bounded on [0, ∞), are established. In the process we obtain new existence results for boundary value problems on compact intervals.
bounded on [0, ∞), are established. In the process we obtain new existence results for boundary value problems on compact intervals.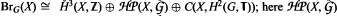 is the group of equivalence classes of principal
is the group of equivalence classes of principal