Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-23T06:35:28.551Z Has data issue: false hasContentIssue false
  • English
  • Français

Tate Cycles on Abelian Varieties with Complex Multiplication

Published online by Cambridge University Press:  20 November 2018

V. Kumar Murty  and
Vijay M. Patankar
V. Kumar Murty
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4. e-mail: murty@math.toronto.edu
Vijay M. Patankar
Affiliation:
International Institute of Information Technology Bangalore, Bangalore, INDIA 560100. e-mail: vijaypatankar@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider Tate cycles on an Abelian variety 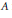$A$ defined over a sufficiently large number field 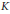$K$ and having complexmultiplication. We show that there is an effective bound 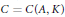$C\,=\,C(A,\,K)$ so that to check whether a given cohomology class is a Tate class on 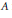$A$, it suffices to check the action of Frobenius elements at primes 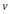$v$ of norm 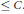$\le \,C$. We also show that for a set of primes 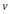$v$ of 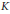$K$ of density 1, the space of Tate cycles on the special fibre 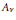${{A}_{v}}$ of the Néron model of 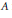$A$ is isomorphic to the space of Tate cycles on 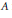$A$ itself.

Keywords

11G1014K22abelian varietiescomplex multiplicationTate cycles
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 1 , 01 February 2015 , pp. 198 - 213
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Katz, N. M. and Messing, W., Some consequences of the Riemann hypothesis for varieties over finite fields. Invent. Math. 23(1974), 73–77.http://dx.doi.org/10.1007/BF01405203 Google Scholar
[2] Lagarias, J. C. and Odlyzko, A. M., Effective versions of the Chebotarev density theorem. In: Algebraic number fields: L-functions and Galois properties (Proc. Sympos., Univ. Durham, Durham, 1975), Academic Press, New York, 1977, pp. 409–464.Google Scholar
[3] Lang, S., Complex multiplication. Grundlehren der Mathematischen Wissenschaften, 255, Springer-Verlag, New York, 1983.Google Scholar
[4] Li, X., The smallest prime that does not split completely in a number field. Algebra Number Theory 6(2012), no. 6, 1061–1096.http://dx.doi.org/10.2140/ant.2012.6.1061 Google Scholar
[5] Murty, M. R. and Murty, V. K., Non-vanishing of L-functions and applications. Progress in Mathematics, 157, Birkhauser, Basel, 1997.Google Scholar
[6] Murty, V. K., The least prime that does not split completely. Forum Math. 6(1994), no. 5, 555–565.Google Scholar
[7] Murty, V. K. and Patankar, V. M., Splitting of Abelian varieties. Internat. Math. Res. Not. 2008, no. 12, Art. ID rnn033.Google Scholar
[8] Pohlmann, H., Algebraic cycles on Abelian varieties of complex multiplication type. Annals of Math 88(1968),161–180.http://dx.doi.org/10.2307/1970570 Google Scholar
[9] Rajan, C. S., On strong multiplicity one for l-adic representations. Internat. Math. Res. Notices 1998, no. 3, 161–172.Google Scholar
[10] Serre, J.-P., Abelian l-adic representations and elliptic curves. W. A. Benjamin Inc., New York-Amsterdam, 1968.Google Scholar
[11] Serre, J.-P., Valeurs propres des endomorphismes de Frobenius (d’apres P. Deligne). Séminaire Bourbaki, no. 446, 1974, Lecture Notes in Math., 431, Springer, Berlin, 1974, pp. 190–204.Google Scholar
[12] Serre, J.-P., Quelques applications du théoème de densit7eacute; de Chebotarev. Inst. Hautes Études Sci. Publ. Math. 54(1981), 323–401.Google Scholar
[13] Serre, J.-P. and Tate, J., Good reduction of Abelian varieties. Ann. of Math. 88(1968), 492–517.http://dx.doi.org/10.2307/1970722 Google Scholar
[14] Shimura, G., Introduction to the arithmetic theory of automorphic functions. Princeton University Press, Princeton, NJ, 1994.Google Scholar
[15] Stark, H. M., Some effective cases of the Brauer-Siegel theorem. Invent. Math. 23(1974), 135–152.http://dx.doi.org/10.1007/BF01405166 Google Scholar
[16] Tate, J. T., Algebraic cycles and poles of zeta functions. In: Arithmetical algebraic geometry, Harper and Row, New York, 1965, pp. 93–110.Google Scholar
[17] Tate, J. T., Conjectures on algebraic cycles in l-adic cohomology. In: Motives (Seattle,WA, 1991), Proc. Symp. Pure Math., 55, Part 1, American Mathematical Society, Providence, RI, 1994, pp. 71–83.Google Scholar
[18] Vaaler, J. D. and Voloch, J. F., The least nonsplit prime in Galois extensions of Q. J. Number Theory 85(2000), no. 2, 320–335. http://dx.doi.org/10.1006/jnth.2000.2551 Google Scholar