Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-26T09:43:53.168Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular G-Monopoles on S1 × Σ

Published online by Cambridge University Press:  20 November 2018

Benjamin H. Smith
Benjamin H. Smith*
Affiliation:
Department of Mathematics and Statistics, McGill University, Montréal, QC e-mail: bh2smith@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This article provides an account of the functorial correspondence between irreducible singular 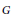$G$-monopoles on 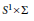${{S}^{1}}\,\times \,\sum $ and 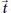$\vec{t}$-stable meromorphic pairs on 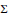$\sum $. A theorem of B.Charbonneau and J. Hurtubise is thus generalized here from unitary to arbitrary compact, connected gauge groups. The required distinctions and similarities for unitary versus arbitrary gauge are clearly outlined, and many parallels are drawn for easy transition. Once the correspondence theorem is complete, the spectral decomposition is addressed.

Keywords

53C0714D20connectioncurvatureinstantonmonopolestabilityBogomolny equationSasakian geometrycameral covers
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 5 , 01 October 2016 , pp. 1096 - 1119
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Charbonneau, B. and Hurtubise, J., Singular Hermitian-Einstein monopoles on the product of a and a Riemann surface. Int. Math. Res. Not. IMRN 2011, no. 1,175–216.http://dx.doi.Org/10.1093/imrn/mq059 Google Scholar
[2] Donagi, R. Y., Spectral covers. In: Current topics in complex algebraic geometry (Berkeley, CA, 1992/93), Math. Sci. Res. Inst. Publ., 28, Cambridge Univ. Press, Cambridge, 1995, pp. 65–86.Google Scholar
[3] Donagi, R. Y. and Gaitsgory, D., The gerbe of Higgs bundles. Transform. Groups 7(2002), no. 2,109–153.http://dx.doi.org/10.1007/s00031-002-0008-z Google Scholar
[4] Donaldson, S. K., A new proof of a theorem ofNarasimhan and Seshadri. J. Differential Geom. 18(1983), no. 2, 269–277.Google Scholar
[5] Donaldson, S. K., Anti self-dual Yang-Mills connections over complex algebraic surfaces and stable vector bundles. Proc. London Math. Soc. 50(1985), no. 1,1–26.http://dx.doi.Org/10.1112/plms/s3-50.1.1 Google Scholar
[6] Donaldson, S. K., Infinite determinants, stable bundles and curvature. Duke Math. J. 54(1987), no. 1, 231–247.http://dx.doi.org/10.1215/S0012-7094-87-05414-7 Google Scholar
[7] Duistermaat, J. J. and Kolk, J. A. C., Lie groups. Universitext, Springer-Verlag, Berlin, 2000.http://dx.doi.org/10.1007/978-3-642-56936-4 Google Scholar
[8] Hurtubise, J. C., The algebraic geometry of the Kostant-Kirillov form. J. London Math. Soc. (2) 56(1997), no. 3, 504–518.http://dx.doi.Org/10.1112/S0024610797005590 Google Scholar
[9] Hurtubise, J. C. and Markman, E., Rank 2-integrable systems ofPrym varieties. Adv. Theor. Math.Phys. 2(1998), no. 3, 633–695.http://dx.doi.org/10.4310/ATMP.1998.v2.n3.a10 Google Scholar
[10] Hurtubise, J. C., Elliptic Sklyanin integrable systems for arbitrary reductive groups. Adv. Theor. Math.Phys. 6(2002), no. 5, 873–978.http://dx.doi.org/10.4310/ATMP.2002.v6.n5.a4 Google Scholar
[11] Kobayashi, S., Differential geometry of complex vector bundles. Princeton University PrePublications of the Mathematical Society of Japan, 15, Kan Memorial Lectures,ss, Princeton, NJ; Iwanami Shoten, Tokyo, 1987.http://dx.doi.org/10.1515/9781400858682 Google Scholar
[12] Kronheimer, P. B., Monopoles and Taub-NUT metrics. Master's Thesis, Oxford University, 1986 Google Scholar
[13] Liibke, M. and Teleman, A., The Kobayashi-Hitchin Correspondence. World Scientific Publisl River Edge, NJ, 1995.http://dx.doi.Org/10.1142/2660 Google Scholar
[14] Narasimhan, M. S. and Seshadri, C. S., Stable and unitary bundles on a compact Riemann surface Ann. of Math. 82(1965), 540–567.http://dx.doi.Org/10.2307/1970710 Google Scholar
[15] Pauly, M., Monopole moduli spaces for compact 3-manifolds. Math. Ann. 311(1998), no. 1,125-46.http://dx.doi.Org/1 0.1007/s002080050180 Google Scholar
[16] Ramanathan, A., Stable principal bundles on a compact Riemann surface. Math. Ann. 213(1975), 129–152.http://dx.doi.org/10.1007/BF01343949 Google Scholar
[17] Scognamillo, R., Prym-Tjurin varieties and the Hitchin map. Math. Ann. 303(1995), no. 1, 47–62.http://dx.doi.Org/1 0.1007/BF01460978 Google Scholar
[18] Scognamillo, R., An elementary approach to the abelianization of the Hitchin system for arbitrary real groups. Compositio Math. 110(1998), no. 1, 17–37.http://dx.doi.Org/10.1023/A:1000235107340 Google Scholar
[19] Simpson, C. T., Constructing variations of Hodge structure using Yang-Mills theory and applications of uniformization. J. Amer. Math. Soc. 1(1988), no. 4, 867–918.http://dx.doi.Org/10.2307/1990994 Google Scholar
[20] Smith, B. H., Singular G-monopoles on circle bundles over a Riemann surface.D. Phil., McGi University, 2015.Google Scholar
[21] Uhlenbeck, K. and Yau, S. T., On the existence of Hermitian Yang-Mills connections in stable bundles. Comm. Pure Appl. Math. 39(1986), no. S, suppl., S257–S293. http://dx.doi.org/10.1002/cpa.3160390714 Google Scholar
[22] Uhlenbeck, K., A note on our previous paper: On the existence of Hermitian Yang-Mills connection stable vector bundles. Comm. Pure Appl. Math. 42(1989), no. 5, 703–707. http://dx.doi.org/10.1002/cpa.3160420505 Google Scholar