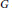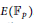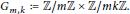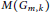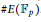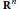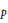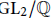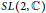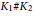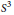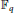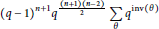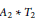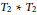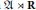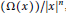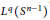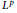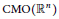Research Article
Monodromy Action on Unknotting Tunnels in Fiber Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1201-1226
-
- Article
-
- You have access
- Export citation
The Frequency of Elliptic Curve Groups over Prime Finite Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 721-761
-
- Article
-
- You have access
- Export citation
On Rational Equivalence in Tropical Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-257
-
- Article
-
- You have access
- Export citation
p–adic Families of Cohomological Modular Forms for Indefinite Quaternion Algebras and the Jacquet–Langlands Correspondence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-998
-
- Article
-
- You have access
- Export citation
The SL(2, C) Casson Invariant for Knots and the Â-polynomial
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-23
-
- Article
-
- You have access
- Export citation
Number of Right Ideals and a q-analogue of Indecomposable Permutations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-503
-
- Article
-
- You have access
- Export citation
Eigenvarieties for Cuspforms Over PEL Type Shimura Varieties With Dense Ordinary Locus
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1227-1256
-
- Article
-
- You have access
- Export citation
Abelian Surfaces with an Automorphism and Quaternionic Multiplication
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 24-43
-
- Article
-
- You have access
- Export citation
Integrable Systems and Torelli Theorems for the Moduli Spaces of Parabolic Bundles and Parabolic Higgs Bundles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 504-520
-
- Article
-
- You have access
- Export citation
On a Linear Refinement of the Prékopa-Leindler Inequality
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 762-783
-
- Article
-
- You have access
- Export citation
Equivariant Map Queer Lie Superalgebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 258-279
-
- Article
-
- You have access
- Export citation
Quotients of A2 * T2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 999-1022
-
- Article
-
- You have access
- Export citation
Sharp Norm Estimates for the Bergman Operator From Weighted Mixed-norm Spaces to Weighted Hardy Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1257-1284
-
- Article
-
- You have access
- Export citation
Centre-valued Index for Toeplitz Operators with Noncommuting Symbols
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1023-1066
-
- Article
-
- You have access
- Export citation
Arithmetic of Degenerating Principal Variations of Hodge Structure: Examples Arising From Mirror Symmetry and Middle Convolution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 280-308
-
- Article
-
- You have access
- Export citation
Optimization Related to Some Nonlocal Problems of Kirchhoff Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 521-540
-
- Article
-
- You have access
- Export citation
Strongly Summable Ultrafilters, Union Ultrafilters, and the Trivial Sums Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 44-66
-
- Article
-
- You have access
- Export citation
Toric Degenerations and Laurent Polynomials Related to Givental's Landau–Ginzburg Models
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 784-815
-
- Article
-
- You have access
- Export citation
Strongly Incompressible Curves
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 541-570
-
- Article
-
- You have access
- Export citation
On the Commutators of Singular Integral Operators with Rough Convolution Kernels
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 816-840
-
- Article
-
- You have access
- Export citation