Article contents
On the Dihedral Main Conjectures of Iwasawa Theory for Hilbert Modular Eigenforms
Published online by Cambridge University Press: 20 November 2018
Abstract
We construct a bipartite Euler system in the sense of Howard for Hilbert modular eigenforms of parallel weight two over totally real fields, generalizing works of Bertolini–Darmon, Longo, Nekovar, Pollack–Weston, and others. The construction has direct applications to Iwasawa's main conjectures. For instance, it implies in many cases one divisibility of the associated dihedral or anticyclotomic main conjecture, at the same time reducing the other divisibility to a certain nonvanishing criterion for the associated 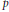 $p$-adic
$p$-adic 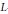 $L$-functions. It also has applications to cyclotomic main conjectures for Hilbert modular forms over
$L$-functions. It also has applications to cyclotomic main conjectures for Hilbert modular forms over 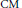 $\text{CM}$ fields via the technique of Skinner and Urban.
$\text{CM}$ fields via the technique of Skinner and Urban.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
- 1
- Cited by




