Hostname: page-component-7479d7b7d-767nl Total loading time: 0 Render date: 2024-07-13T16:28:56.597Z Has data issue: false hasContentIssue false
  • English
  • Français

More Ramsey theory for highly connected monochromatic subgraphs

Part of: Set theory

Published online by Cambridge University Press:  24 November 2023

Michael Hrušák ,
Saharon Shelah Open the ORCID record for Saharon Shelah [Opens in a new window]  and
Jing Zhang
Michael Hrušák
Affiliation:
Centro de Ciencas Matemáticas, Universidad Nacional Autónoma de México (UNAM), A.P. 61-3, Xangari, Morelia, Michoacán 58089, México e-mail: michael@matmor.unam.mx
Saharon Shelah
Affiliation:
Department of Mathematics, Rutgers University, Hill Center, Piscataway, NJ 08854-8019, United States and Institute of Mathematics, Hebrew University, Givat Ram, Jerusalem 91904, Israel e-mail: shelah@math.rutgers.edu
Jing Zhang*
Affiliation:
Department of Mathematics, University of Toronto, Bahen Centre, 40 St. George Street, Room 6290, Toronto, ON M5S 2E4, Canada
*
e-mail: jingzhangjz13@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

An infinite graph is said to be highly connected if the induced subgraph on the complement of any set of vertices of smaller size is connected. We continue the study of weaker versions of Ramsey’s theorem on uncountable cardinals asserting that if we color edges of the complete graph, we can find a large highly connected monochromatic subgraph. In particular, several questions of Bergfalk, Hrušák, and Shelah (2021, Acta Mathematica Hungarica 163, 309–322) are answered by showing that assuming the consistency of suitable large cardinals, the following are relatively consistent with ZFC:

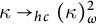  • • $\kappa \to _{hc} (\kappa )^2_\omega $ for every regular cardinal 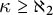$\kappa \geq \aleph _2$,

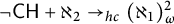  • • $\neg \mathsf {CH}+ \aleph _2 \to _{hc} (\aleph _1)^2_\omega $.

Building on a work of Lambie-Hanson (2023, Fundamenta Mathematicae. 260(2):181–197), we also show that

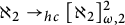  • • $\aleph _2 \to _{hc} [\aleph _2]^2_{\omega ,2}$ is consistent with 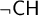$\neg \mathsf {CH}$.

To prove these results, we use the existence of ideals with strong combinatorial properties after collapsing suitable large cardinals.

Keywords

Highly connected graphsaturated idealpartition relationsforcing

MSC classification

Primary: 03E02: Partition relations 03E10: Ordinal and cardinal numbers
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 15
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research of the first author was partially supported by a PAPIIT grant IN101323 and CONACyT grant A1-S-16164. Research of the second author was partially supported by the NSF grant DMS 1833363 and by the Israel Science Foundation (ISF) grant 1838/19. Research of the third author was supported by the European Research Council (Grant Agreement No. ERC-2018-StG 802756) and NSERC grants RGPIN-2019-04311, RGPIN-2021-03549, and RGPIN-2016-06541. The paper appears as number 1242 on the second author’s publications list.

References

Abraham, U., Aronszajn trees on  ${\aleph}_2$  and  ${\aleph}_3$ . Ann. Pure Appl. Logic 24(1983), no. 3, 213–230.CrossRefGoogle Scholar
Bannister, N., Bergfalk, J., Moore, J. T., and Todorcevic, S., A descriptive approach to higher derived limits. Journal of European Mathematical Society, to appear, 2023. arXiv:2203.00165 Google Scholar
Bergfalk, J., Ramsey theory for monochromatically well-connected subsets . Fund. Math. 249(2020), no. 1, 95–103.CrossRefGoogle Scholar
Bergfalk, J., Hrušák, M., and Lambie-Hanson, C., Simultaneously vanishing higher derived limits without large cardinals . J. Math. Log. 23(2023), no. 1, Article no. 2250019, 40 pp.CrossRefGoogle Scholar
Bergfalk, J., Hrušák, M., and Shelah, S., Ramsey theory for highly connected monochromatic subgraphs . Acta Math. Hungar. 163(2021), no. 1, 309–322.CrossRefGoogle Scholar
Bergfalk, J. and Lambie-Hanson, C., Simultaneously vanishing higher derived limits . Forum Math. Pi 9(2021), Article no. E4, 31 pp.CrossRefGoogle Scholar
Cummings, J., Iterated forcing and elementary embeddings . In: Handbook of set theory, Vols. 1–3, Springer, Dordrecht, 2010, pp. 775–883.CrossRefGoogle Scholar
Erdős, P. and Hajnal, A., On complete topological subgraphs of certain graphs . Ann. Univ. Sci. Budapest. Eötvös Sect. Math. 7(1964), 143–149.Google Scholar
Foreman, M., Ideals and generic elementary embeddings . In: Handbook of set theory. Vols. 1–3, Springer, Dordrecht, 2010, pp. 885–1147.CrossRefGoogle Scholar
Foreman, M., Magidor, M., and Shelah, S., Martin’s maximum, saturated ideals, and nonregular ultrafilters I . Ann. Math. 127(1988), no. 1, 1–47.CrossRefGoogle Scholar
Galvin, F., Jech, T., and Magidor, M., An ideal game . J. Symb. Log. 43(1978), no. 2, 284–292.CrossRefGoogle Scholar
Gitman, V., Ramsey-like cardinals . J. Symb. Log. 76(2011), no. 2, 519–540.CrossRefGoogle Scholar
Hugh Woodin, W., Davis, J., and Rodríguez, D., The HOD dichotomy . In: Appalachian set theory: 2006–2012, London Mathematical Society Lecture Note Series, 406, Cambridge University Press, Cambridge, 2013, pp. 397–418.Google Scholar
Jech, T. and Prikry, K., On ideals of sets and the power set operation . Bull. Amer. Math. Soc. 82(1976), no. 4, 593–595.CrossRefGoogle Scholar
Komjáth, P. and Shelah, S., Monocolored topological complete graphs in colorings of uncountable complete graphs . Acta Math. Hungar. 163(2021), no. 1, 71–84.CrossRefGoogle Scholar
Lambie-Hanson, C., A note on highly connected and well-connected Ramsey theory. Fundamenta Mathematicae. 260(2023), no. 2, 181–197.Google Scholar
Laver, R., Precipitousness in forcing extensions . Israel J. Math. 48(1984), nos. 2–3, 97–108.CrossRefGoogle Scholar
Mitchell, W., Aronszajn trees and the independence of the transfer property . Ann. Math. Logic 5(1972/73), 21–46.CrossRefGoogle Scholar
Veličković, B. and Vignati, A., Non-vanishing higher derived limits. Communications in Contemporary Mathematics, to appear 2023. https://doi.org/10.1142/S0219199723500311CrossRefGoogle Scholar