Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-06-24T02:46:20.456Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal or Greatest Homomorphic Images of Given Type

Published online by Cambridge University Press:  20 November 2018

Takayuki Tamura
Takayuki Tamura*
Affiliation:
University of California, Davis, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Q be a quasi-ordered set with respect to ⩽ ; that is, the order ⩽ is reflexive and transitive. An element a of Q is called maximal (minimal) if

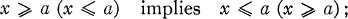
a is called greatest (smallest) if

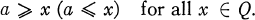
Obviously a greatest (smallest) element is maximal (minimal). A greatest (smallest) element in a partially ordered set is unique, but it is not necessarily unique in a quasi-ordered set.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 264 - 271
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Vol. I, Math. Surveys No. 7 (Amer. Math. Soc, Providence, R.I., 1961).Google Scholar
2. Kimura, N., On some existence theorems on multiplication system I, Greatest quotient, Proc. Japan Acad., 34 (1958), 305–309.Google Scholar
3. Petrich, M., The maximal semilattice decomposition of a semigroup, Math. Z., 85 (1964), 68–82.Google Scholar
4. Plemmons, R., Semigroups with a maximal semigroup with zero homomorphic image, Notices Amer. Math. Soc, 11 (7) (1964), 751.Google Scholar
5. Plemmons, R. J. and Tamura, T., Semigroups with a maximal homomorphic image having zero, Proc. Japan Acad., 41 (1965), 681–685.Google Scholar
6. Tamura, T. and Kimura, N., On decompositions of a commutative semigroup, Kôdai Math. Sem., Rep. 4 (1954), 182–225.Google Scholar
7. Tamura, T. and Kimura, N., Existence of greatest decomposition of a semigroup, Kôdai Math. Sem. Rep., 7 (1955), 83–84.Google Scholar
8. Tamura, T., The theory of operations on binary relations, Trans. Amer. Math. Soc, 120 (1965), 343–358.Google Scholar
9. Yamada, M., On the greatest semilattice decomposition of a semigroup, Kôdai Math. Sem. Rep., 7 (1955), 59–62.Google Scholar