Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-05-10T15:43:30.568Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal Homotopy Lie Subgroups of Maximal Rank

Published online by Cambridge University Press:  20 November 2018

John A. Frohliger
John A. Frohliger*
Affiliation:
St. Norbert College, De Pere, Wisconsin
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a compact connected Lie group with H a connected subgroup of maximal rank. Suppose there exists a compact connected Lie subgroup K with H ⊂ K ⊂ G. Then there exists a smooth fiber bundle G/H → G/K with K/H as the fiber. (See for example [13].) This can be incorporated into a diagram involving the classifying spaces as follows:

(1)

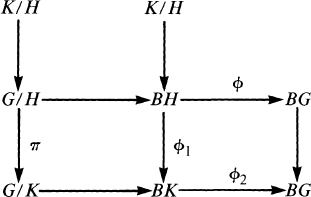
Here π, ϕ, ϕ1 and ϕ2 denote fibrations. We also know that the homogeneous spaces and the Lie groups, which are homotopy equivalent to the loop spaces of their respective classifying spaces, are homotopy equivalent to connected finite complexes.

Now suppose H is a maximal subgroup. Can there still exist spaces, which we will call BK, K/H, and G/K, and fibrations so that diagram (1) is still valid? This paper will show that in many cases either G/K or K/H will be homo topically trivial.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 4 , 01 August 1988 , pp. 769 - 787
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Becker, J. C. and Gottlieb, D. H., Applications of the evaluation map and transfer map theorems, Math Ann. 211 (1974), 277–288.Google Scholar
2. Benson, C. T. and Grove, L. C., Finite reflection groups (Bogden and Quigley, Tarry town, N.Y., 1971).Google Scholar
3. Borel, A., La cohomologie mod 2 des certains espaces homogènes, Comm. Math. Helv. 27 (1953), 165–197.Google Scholar
4. Borel, A., Sur la cohomologie des espaces fibres principaux et des espaces homogènes des groupes de Lie compacts, Ann. of Math. 57 (1953), 115–207.Google Scholar
5. Borel, A., Topics in the homology theory of fibre bundles (Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar
6. Borel, A. and DeSiebenthal, J., Les sous-groupes fermés de rang maximum des groupes de Lie clos, Comm. Math. Helv. 23 (1949), 200–221.Google Scholar
7. Casson, A. and Gottlieb, D. H., Fibrations with compact fibres, Amer. J. Math. 99 (1977), 159–189.Google Scholar
8. Clark, A. and Ewing, J., The realization of polynomial algebras as cohomology rings, Pacific J. Math. 50(1974), 425–434.Google Scholar
9. Frohliger, J. A., Maximal homotopy Lie subgroups of maximal rank, Ph.D. Thesis, Purdue University (1983).Google Scholar
10. Quinn, F. S., Surgery on Poincaré and normal spaces, Bull. Amer. Math. Soc. 78 (1972), 262–267.Google Scholar
11. Rector, D. L., Subgroups of finite dimensional topological groups, J. Pure and Appl. Alg. 1 (1971), 253–273.Google Scholar
12. Schultz, R., Compact fiberings of homogeneous spaces I, Comp. Math. 43 (1981), 181–215.Google Scholar
13. Steenrod, N., The topology of fibre bundles (Princeton University Press, Princeton, N. J., 1951).CrossRefGoogle Scholar
14. Shepard, G. C. and Todd, J. A., Finite unitary and reflection groups, Can. J. Math. 6 (1954), 274–304.Google Scholar
15. Spanier, E. H., Algebraic topology (McGraw-Hill, New York, 1967).Google Scholar
16. Wall, C. T. C., Poincaré complexes, Ann. of Math. 86 (1967), 213–245.Google Scholar
17. Wilkerson, C., Classifying spaces, Steenrod operations and algebraic closure, Topology 16 (1977), 227–237.Google Scholar