Article contents
Mallows permutations as stable matchings
Published online by Cambridge University Press: 27 July 2020
Abstract
We show that the Mallows measure on permutations of
 $1,\dots ,n$
arises as the law of the unique Gale–Shapley stable matching of the random bipartite graph with vertex set
$1,\dots ,n$
arises as the law of the unique Gale–Shapley stable matching of the random bipartite graph with vertex set 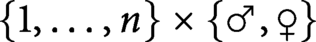 conditioned to be perfect, where preferences arise from the natural total ordering of the vertices of each gender but are restricted to the (random) edges of the graph. We extend this correspondence to infinite intervals, for which the situation is more intricate. We prove that almost surely, every stable matching of the random bipartite graph obtained by performing Bernoulli percolation on the complete bipartite graph
conditioned to be perfect, where preferences arise from the natural total ordering of the vertices of each gender but are restricted to the (random) edges of the graph. We extend this correspondence to infinite intervals, for which the situation is more intricate. We prove that almost surely, every stable matching of the random bipartite graph obtained by performing Bernoulli percolation on the complete bipartite graph
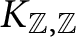 $K_{{\mathbb Z},{\mathbb Z}}$
falls into one of two classes: a countable family
$K_{{\mathbb Z},{\mathbb Z}}$
falls into one of two classes: a countable family
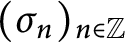 $(\sigma _n)_{n\in {\mathbb Z}}$
of tame stable matchings, in which the length of the longest edge crossing k is
$(\sigma _n)_{n\in {\mathbb Z}}$
of tame stable matchings, in which the length of the longest edge crossing k is
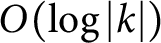 $O(\log |k|)$
as
$O(\log |k|)$
as
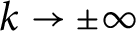 $k\to \pm \infty $
, and an uncountable family of wild stable matchings, in which this length is
$k\to \pm \infty $
, and an uncountable family of wild stable matchings, in which this length is
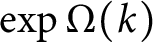 $\exp \Omega (k)$
as
$\exp \Omega (k)$
as
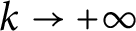 $k\to +\infty $
. The tame stable matching
$k\to +\infty $
. The tame stable matching
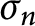 $\sigma _n$
has the law of the Mallows permutation of
$\sigma _n$
has the law of the Mallows permutation of
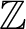 ${\mathbb Z}$
(as constructed by Gnedin and Olshanski) composed with the shift
${\mathbb Z}$
(as constructed by Gnedin and Olshanski) composed with the shift
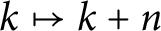 $k\mapsto k+n$
. The permutation
$k\mapsto k+n$
. The permutation
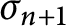 $\sigma _{n+1}$
dominates
$\sigma _{n+1}$
dominates
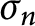 $\sigma _{n}$
pointwise, and the two permutations are related by a shift along a random strictly increasing sequence.
$\sigma _{n}$
pointwise, and the two permutations are related by a shift along a random strictly increasing sequence.
MSC classification
- Type
- Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
This work was carried out while O.A. was visiting and T.H. was an intern at Microsoft Research, Redmond. O.A. was supported in part by NSERC. T.H. was also supported by a Microsoft Research Ph.D. Fellowship.
References
- 2
- Cited by





