Hostname: page-component-848d4c4894-8kt4b Total loading time: 0 Render date: 2024-07-02T16:25:59.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower bounds on Bourgain’s constant for harmonic measure

Part of: Higher-dimensional theory Classical measure theory Markov processes

Published online by Cambridge University Press:  27 October 2023

Matthew Badger  and
Alyssa Genschaw
Matthew Badger*
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, CT, United States
Alyssa Genschaw
Affiliation:
Mathematics Department, Milwaukee School of Engineering, Milwaukee, WI, United States e-mail: genschaw@msoe.edu
*
e-mail: matthew.badger@uconn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

For every 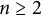$n\geq 2$, Bourgain’s constant $b_n$ is the largest number such that the (upper) Hausdorff dimension of harmonic measure is at most 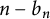$n-b_n$ for every domain in 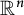$\mathbb {R}^n$ on which harmonic measure is defined. Jones and Wolff (1988, Acta Mathematica 161, 131–144) proved that 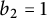$b_2=1$. When 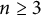$n\geq 3$, Bourgain (1987, Inventiones Mathematicae 87, 477–483) proved that 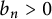$b_n>0$ and Wolff (1995, Essays on Fourier analysis in honor of Elias M. Stein (Princeton, NJ, 1991), Princeton University Press, Princeton, NJ, 321–384) produced examples showing 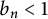$b_n<1$. Refining Bourgain’s original outline, we prove that

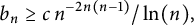$$\begin{align*}b_n\geq c\,n^{-2n(n-1)}/\ln(n),\end{align*}$$
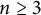for all $n\geq 3$, where $c>0$ is a constant that is independent of n. We further estimate 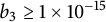$b_3\geq 1\times 10^{-15}$ and 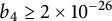$b_4\geq 2\times 10^{-26}$.

Keywords

Harmonic measureHausdorff dimensionBourgain’s estimateFrostman’s lemmanet measures

MSC classification

Primary: 31B15: Potentials and capacities, extremal length
Secondary: 28A75: Length, area, volume, other geometric measure theory 31B25: Boundary behavior 60J65: Brownian motion
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 20
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

M. Badger was partially supported by NSF DMS grant 2154047.

References

Axler, S., Bourdon, P., and Ramey, W., Harmonic function theory. 2nd ed., Graduate Texts in Mathematics, 137, Springer, New York, 2001.CrossRefGoogle Scholar
Azzam, J., Dimension drop for harmonic measure on Ahlfors regular boundaries . Potential Anal. 53(2020), no. 3, 1025–1041.CrossRefGoogle Scholar
Azzam, J., Hofmann, S., Martell, J. M., Mayboroda, S., Mourgoglou, M., Tolsa, X., and Volberg, A., Rectifiability of harmonic measure . Geom. Funct. Anal. 26(2016), no. 3, 703–728.CrossRefGoogle Scholar
Badger, M. and Genschaw, A., Hausdorff dimension of caloric measure, to appear in Amer. J. Math., 2023. arXiv:2108.12340v2Google Scholar
Batakis, A., Harmonic measure of some cantor type sets . Ann. Acad. Sci. Fenn. Math. 21(1996), no. 2, 255–270.Google Scholar
Batakis, A. and Zdunik, A., Hausdorff and harmonic measures on non-homogeneous cantor sets . Ann. Acad. Sci. Fenn. Math. 40(2015), no. 1, 279–303.CrossRefGoogle Scholar
Bishop, C. J., Some questions concerning harmonic measure , Partial differential equations with minimal smoothness and applications (Chicago, IL, 1990), The IMA Volumes in Mathematics and Its Applications, 42, Springer, New York, 1992, pp. 89–97.CrossRefGoogle Scholar
Bishop, C. J., Review of harmonic measure . Bull. Amer. Math. Soc. 44(2007), no. 2, 267–276.CrossRefGoogle Scholar
Bishop, C. J. and Peres, Y., Fractals in probability and analysis, Cambridge Studies in Advanced Mathematics, 162, Cambridge University Press, Cambridge, 2017.Google Scholar
Bourgain, J., On the Hausdorff dimension of harmonic measure in higher dimension . Invent. Math. 87(1987), no. 3, 477–483.CrossRefGoogle Scholar
Carleson, L., On the support of harmonic measure for sets of cantor type . Ann. Acad. Sci. Fenn. Ser. A I Math. 10(1985), 113–123.CrossRefGoogle Scholar
Doob, J. L., Classical potential theory and its probabilistic counterpart, Classics in Mathematics, Springer, Berlin, 2001, Reprint of the 1984 edition.CrossRefGoogle Scholar
Falconer, K., Techniques in fractal geometry, John Wiley & Sons, Chichester, 1997.Google Scholar
Filoche, M., Grebenkov, D. S., Andrade, J. S., and Sapoval, B., Passivation of irregular surfaces accessed by diffusion . Proc. Natl. Acad. Sci. 105(2008), no. 22, 7636–7640.CrossRefGoogle ScholarPubMed
Garnett, J. B. and Marshall, D. E., Harmonic measure, New Mathematical Monographs, 2, Cambridge University Press, Cambridge, 2005.CrossRefGoogle Scholar
Grebenkov, D. S., Lebedev, A. A., Filoche, M., and Sapoval, B., Multifractal properties of the harmonic measure on Koch boundaries in two and three dimensions . Phys. Rev. E 71(2005), 056121.CrossRefGoogle ScholarPubMed
Helms, L. L., Potential theory, Universitext, Springer, London, 2009.CrossRefGoogle Scholar
Hofmann, S. and Martell, J. M., Uniform rectifiability and harmonic measure I: uniform rectifiability implies Poisson kernels in ${L}^p$ . Ann. Sci. Éc. Norm. Supér. (4) 47(2014), no. 3, 577–654.CrossRefGoogle Scholar
Jones, P. W. and Wolff, T. H., Hausdorff dimension of harmonic measures in the plane . Acta Math. 161(1988), nos. 1–2, 131–144.CrossRefGoogle Scholar
Kaufman, R. and Jang-Mei, W., On the snowflake domain . Ark. Mat. 23(1985), no. 1, 177–183.CrossRefGoogle Scholar
Lewis, J. L., Verchota, G. C., and Vogel, A. L., Wolff snowflakes . Pacific J. Math. 218(2005), no. 1, 139–166.CrossRefGoogle Scholar
Li, Y.-C., A note on an identity of the gamma function and Stirling’s formula . Real Anal. Exchange. 32(2006/07), no. 1, 267–271.Google Scholar
Makarov, N. G., On the distortion of boundary sets under conformal mappings , Proc. Lond. Math. Soc. (3) 51 (1985), no. 2, 369–384.CrossRefGoogle Scholar
Mattila, P., Geometry of sets and measures in Euclidean spaces: fractals and rectifiability, Cambridge Studies in Advanced Mathematics, 44, Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Mattila, P., Morán, M., and Rey, J.-M., Dimension of a measure . Stud. Math. 142(2000), no. 3, 219–233.CrossRefGoogle Scholar
Mörters, P. and Peres, Y., Brownian motion, Cambridge Series in Statistical and Probabilistic Mathematics, Cambridge University Press, Cambridge, 2010, With an appendix by Oded Schramm and Wendelin Werner.Google Scholar
Øksendal, B., Brownian motion and sets of harmonic measure zero . Pacific J. Math. 95(1981), no. 1, 179–192.CrossRefGoogle Scholar
Rogers, C. A., Hausdorff measures, Cambridge Mathematical Library, Cambridge University Press, Cambridge, 1998, Reprint of the 1970 original, With a foreword by K. J. Falconer.Google Scholar
Wolff, T. H., Plane harmonic measures live on sets of $\sigma$ -finite length . Ark. Mat. 31(1993), no. 1, 137–172.CrossRefGoogle Scholar
Wolff, T. H., Counterexamples with harmonic gradients in R3 . In: Essays on Fourier analysis in honor of Elias M. Stein (Princeton, NJ, 1991), Princeton Mathematical Series, 42, Princeton University Press, Princeton, NJ, 1995, pp. 321–384.CrossRefGoogle Scholar