Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-05-01T11:38:20.977Z Has data issue: false hasContentIssue false
  • English
  • Français

Isogeny graphs on superspecial abelian varieties: eigenvalues and connection to Bruhat–Tits buildings

Part of: Arithmetic problems. Diophantine geometry Discontinuous groups and automorphic forms Arithmetic algebraic geometry Finite geometry and special incidence structures

Published online by Cambridge University Press:  20 October 2023

Yusuke Aikawa ,
Ryokichi Tanaka Open the ORCID record for Ryokichi Tanaka [Opens in a new window]  and
Takuya Yamauchi Open the ORCID record for Takuya Yamauchi [Opens in a new window]
Yusuke Aikawa
Affiliation:
Graduate School of Information Science and Technology, The University of Tokyo, Tokyo 113-8656, Japan e-mail: aikawa@mist.i.u-tokyo.ac.jp
Ryokichi Tanaka
Affiliation:
Department of Mathematics, Kyoto University, Kyoto 606-8502, Japan e-mail: rtanaka@math.kyoto-u.ac.jp
Takuya Yamauchi*
Affiliation:
Mathematical Institute, Tohoku University, Sendai 980-8578, Japan
*
e-mail: takuya.yamauchi.c3@tohoku.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

We study for each fixed integer 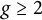$g \ge 2$, for all primes 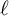$\ell $ and p with 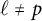$\ell \neq p$, finite regular directed graphs associated with the set of equivalence classes of 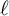$\ell $-marked principally polarized superspecial abelian varieties of dimension g in characteristic p, and show that the adjacency matrices have real eigenvalues with spectral gaps independent of p. This implies a rapid mixing property of natural random walks on the family of isogeny graphs beyond the elliptic curve case and suggests a potential construction of the Charles–Goren–Lauter-type cryptographic hash functions for abelian varieties. We give explicit lower bounds for the gaps in terms of the Kazhdan constant for the symplectic group when 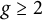$g \ge 2$. As a byproduct, we also show that the finite regular directed graphs constructed by Jordan and Zaytman also has the same property.

Keywords

Isogeny graphscryptographic hash functionssuperspecial abelian varietiesisogeny graphsBruhat—Tits buildings

MSC classification

Primary: 11F55: Other groups and their modular and automorphic forms (several variables) 11G10: Abelian varieties of dimension $> 1$ 14G50: Applications to coding theory and cryptography 51E24: Buildings and the geometry of diagrams
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 26
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Y.A. is supported by JST, ACT-X Grant Number JPMJAX2001, Japan. R.T. is partially supported by JSPS Grant-in-Aid for Scientific Research JP20K03602 and JST, ACT-X Grant Number JPMJAX190J, Japan. T.Y. is partially supported by JSPS KAKENHI Grant Number (B) 19H01778.

References

Bekka, B., de la Harpe, P., and Valette, A., Kazhdan’s property (T), New Mathematical Monographs, 11, Cambridge University Press, Cambridge, 2008.CrossRefGoogle Scholar
Castryck, W., Decru, T., and Smith, B., Hash functions from superspecial genus-2 curves using Richelot isogenies . J. Math. Cryptol. 14(2020), no. 1, 268–292.CrossRefGoogle Scholar
Chai, C-L. and Faltings, G., Degeneration of abelian varieties, with an appendix by David Mumford, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 22, Springer, Berlin, 1990, xii + 316 pp.Google Scholar
Charles, D.-X., Lauter, K., and Goren, E.-Z., Cryptographic hash functions from expander graphs . J. Cryptol. 22(2009), no. 1, 93–113.CrossRefGoogle Scholar
Edixhoven, B., van der Geer, G., and Moonen, B., Abelian varieties. Draft for a book on abelian varieties. Available at http://page.mi.fu-berlin.de/elenalavanda/BMoonen.pdf.Google Scholar
Faltings, G., Finiteness theorems for abelian varieties over number fields . In: Shipz, E. (ed.), Arithmetic geometry (Storrs, Conn., 1984), Springer, New York, 1986, pp. 9–27.CrossRefGoogle Scholar
Florit, E. and Smith, B., An atlas of the Richelot isogeny graph . RIMS Kôkyûroku Bessatsu. B90(2022), 195–219.Google Scholar
Florit, E. and Smith, B., Automorphisms and isogeny graphs of abelian varieties, with applications to the Superspecial Richelot isogeny graph . In: Arithmetic, geometry, cryptography, and coding theory 2021, Contemporary Mathematics, 779, American Mathematical Society, Providence, RI, 2022, pp. 103–132.CrossRefGoogle Scholar
Garrett, P., Buildings and classical groups, Chapman & Hall, London, 1997, xii + 373 pp.CrossRefGoogle Scholar
Ghitza, A., Hecke eigenvalues of Siegel modular forms (mod $p$ ) and of algebraic modular forms . J. Number Theory 106(2004), no. 2, 345–384.CrossRefGoogle Scholar
Ibukiyama, T., Principal polarizations of supersingular abelian surfaces . J. Math. Soc. Japan. 72(2020), no. 4, 1161–1180.CrossRefGoogle Scholar
Ibukiyama, T., Katsura, T., and Oort, F., Supersingular curves of genus two and class numbers . Compos. Math. 57(1986), no. 2, 127–152.Google Scholar
Jordan, B.-W. and Zaytman, Y., Isogeny graphs of superspecial abelian varieties and Brandt matrices. Preprint, 2023. arXiv:2005.09031 Google Scholar
Katsura, T. and Takashima, K., Counting Richelot isogenies between superspecial abelian surfaces . In: Galbraith, S. D. (ed.), Proceedings of the fourteenth algorithmic number theory symposium. Vol. 4, The Open Book Series, 1, Mathematical Sciences Publishers, Berkeley, CA, 2020, pp. 283–300.Google Scholar
Li, K.-Z. and Oort, F., Moduli of supersingular abelian varieties, Lecture Notes in Mathematics, 1680, Springer, Berlin, 1998, iv + 116 pp.CrossRefGoogle Scholar
Lubetzky, E. and Peres, Y., Cutoff on all Ramanujan graphs . Geom. Funct. Anal. 26(2016), no. 4, 1190–1216.CrossRefGoogle Scholar
Milne, J.-S., Abelian varieties . In: Arithmetic geometry (Storrs, Conn., 1984), Springer, New York, 1986, pp. 103–150.CrossRefGoogle Scholar
Mumford, D., Abelian varieties, Tata Institute of Fundamental Research Studies in Mathematics, 5, Published for the Tata Institute of Fundamental Research, Bombay; Oxford University Press, London, 1970, viii + 242 pp.Google Scholar
Oh, H., Uniform pointwise bounds for matrix coefficients of unitary representations and applications to Kazhdan constants . Duke Math. J. 113(2002), no. 1, 133–192.CrossRefGoogle Scholar
Pizer, A.-K., Ramanujan graphs and Hecke operators . Bull. Amer. Math. Soc. (N.S.) 23(1990), no. 1, 127–137.CrossRefGoogle Scholar
Pizer, A.-K., Ramanujan graphs . In: Computational perspectives on number theory (Chicago, IL, 1995), AMS/IP Studies in Advanced Mathematics, 7, American Mathematical Society, Providence, RI, 1998, pp. 159–178.Google Scholar
Platonov, V. and Rapinchuk, A., Algebraic groups and number theory, Translated from the 1991 Russian original by Rachel Rowen, Pure and Applied Mathematics, 139, Academic Press, Boston, MA, 1994, xii + 614 pp.Google Scholar
Shemanske, T. R., The arithmetic and combinatorics of buildings for ${Sp}_n$ . Trans. Amer. Math. Soc. 359(2007), no. 7, 3409–3423.CrossRefGoogle Scholar
Silverman, J.-H., The arithmetic of elliptic curves. 2nd ed., Graduate Texts in Mathematics, 106, Springer, Dordrecht, 2009, xx + 513 pp.CrossRefGoogle Scholar
Tate, J., Endomorphisms of abelian varieties over finite fields . Invent. Math. 2(1966), 134–144.CrossRefGoogle Scholar
van der Geer, G., Siegel modular forms and their applications . In: The 1–2–3 of modular forms, Universitext, Springer, Berlin, 2008, pp. 181–245.Google Scholar