Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liu, Shiping
Münch, Florentin
and
Peyerimhoff, Norbert
2018.
Bakry–Émery curvature and diameter bounds on graphs.
Calculus of Variations and Partial Differential Equations,
Vol. 57,
Issue. 2,
Erbar, Matthias
and
Fathi, Max
2018.
Poincaré, modified logarithmic Sobolev and isoperimetric inequalities for Markov chains with non-negative Ricci curvature.
Journal of Functional Analysis,
Vol. 274,
Issue. 11,
p.
3056.
Fathi, Max
and
Shu, Yan
2018.
Curvature and transport inequalities for Markov chains in discrete spaces.
Bernoulli,
Vol. 24,
Issue. 1,
LIU, SHIPING
and
PEYERIMHOFF, NORBERT
2018.
Eigenvalue Ratios of Non-Negatively Curved Graphs.
Combinatorics, Probability and Computing,
Vol. 27,
Issue. 5,
p.
829.
Liu, Shiping
Münch, Florentin
and
Peyerimhoff, Norbert
2019.
Curvature and Higher Order Buser Inequalities for the Graph Connection Laplacian.
SIAM Journal on Discrete Mathematics,
Vol. 33,
Issue. 1,
p.
257.
Spener, Adrian
Weber, Frederic
and
Zacher, Rico
2019.
Curvature-dimension inequalities for non-local operators in the discrete setting.
Calculus of Variations and Partial Differential Equations,
Vol. 58,
Issue. 5,
Ache, Antonio G.
and
Warren, Micah W.
2019.
Ricci curvature and the manifold learning problem.
Advances in Mathematics,
Vol. 342,
Issue. ,
p.
14.
Horn, Paul
2019.
A Spacial Gradient Estimate for Solutions to the Heat Equation on Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 33,
Issue. 2,
p.
958.
Cushing, David
Kamtue, Supanat
Peyerimhoff, Norbert
and
Watson May, Leyna
2020.
Quartic graphs which are Bakry-Émery curvature sharp.
Discrete Mathematics,
Vol. 343,
Issue. 3,
p.
111767.
Cushing, David
Liu, Shiping
and
Peyerimhoff, Norbert
2020.
Bakry–Émery Curvature Functions on Graphs.
Canadian Journal of Mathematics,
Vol. 72,
Issue. 1,
p.
89.
Münch, Florentin
and
Rose, Christian
2020.
Spectrally positive Bakry-Émery Ricci curvature on graphs.
Journal de Mathématiques Pures et Appliquées,
Vol. 143,
Issue. ,
p.
334.
Mazón, José M.
Solera, Marcos
and
Toledo, Julián
2020.
The heat flow on metric random walk spaces.
Journal of Mathematical Analysis and Applications,
Vol. 483,
Issue. 2,
p.
123645.
Benson, Brian
Ralli, Peter
and
Tetali, Prasad
2021.
Volume Growth, Curvature, and Buser-Type Inequalities in Graphs.
International Mathematics Research Notices,
Vol. 2021,
Issue. 22,
p.
17091.
Siconolfi, Viola
2021.
Ricci curvature, graphs and eigenvalues.
Linear Algebra and its Applications,
Vol. 620,
Issue. ,
p.
242.
Weber, Frederic
and
Zacher, Rico
2021.
The entropy method under curvature-dimension conditions in the spirit of Bakry-Émery in the discrete setting of Markov chains.
Journal of Functional Analysis,
Vol. 281,
Issue. 5,
p.
109061.
Shi, Yongjie
and
Yu, Chengjie
2022.
Comparison of Steklov eigenvalues and Laplacian eigenvalues on graphs.
Proceedings of the American Mathematical Society,
Vol. 150,
Issue. 4,
p.
1505.
Liu, Shiping
Münch, Florentin
and
Peyerimhoff, Norbert
2022.
Rigidity properties of the hypercube via Bakry–Émery curvature.
Mathematische Annalen,
Samson, Paul-Marie
2022.
Entropic curvature on graphs along Schrödinger bridges at zero temperature.
Probability Theory and Related Fields,
Vol. 184,
Issue. 3-4,
p.
859.
Cushing, David
Kangaslampi, Riikka
Lipiäinen, Valtteri
Liu, Shiping
and
Stagg, George W.
2022.
The Graph Curvature Calculator and the Curvatures of Cubic Graphs.
Experimental Mathematics,
Vol. 31,
Issue. 2,
p.
583.
Mazón, José M.
Solera, Marcos
and
Toledo, Julián
2022.
Gradient flows in metric random walk spaces.
SeMA Journal,
Vol. 79,
Issue. 1,
p.
3.
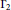 ${{\Gamma }_{2}}$-calculus (of Bakry-Émery) seems to be that it is fairly straightforward to compute this notion of curvature parameter for several specific graphs of interest, particularly, abelian groups, slices of the hypercube, and the symmetric group under various sets of generators. We further develop this notion by deriving Buser-type inequalities (à la Ledoux), relating functional and isoperimetric constants associated with a graph. Our derivations provide a tight bound on the Cheeger constant (i.e., the edge-isoperimetric constant) in terms of the spectral gap, for graphs with nonnegative curvature, particularly, the class of abelian Cayley graphs, a result of independent interest.
${{\Gamma }_{2}}$-calculus (of Bakry-Émery) seems to be that it is fairly straightforward to compute this notion of curvature parameter for several specific graphs of interest, particularly, abelian groups, slices of the hypercube, and the symmetric group under various sets of generators. We further develop this notion by deriving Buser-type inequalities (à la Ledoux), relating functional and isoperimetric constants associated with a graph. Our derivations provide a tight bound on the Cheeger constant (i.e., the edge-isoperimetric constant) in terms of the spectral gap, for graphs with nonnegative curvature, particularly, the class of abelian Cayley graphs, a result of independent interest.



