Article contents
Categorical Aspects of Quantum Groups: Multipliers and Intrinsic Groups
Published online by Cambridge University Press: 20 November 2018
Abstract
We show that the assignment of the (left) completely bounded multiplier algebra 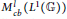 $M_{cb}^{l}({{L}^{1}}(\mathbb{G}))$ to a locally compact quantum group
$M_{cb}^{l}({{L}^{1}}(\mathbb{G}))$ to a locally compact quantum group  $\mathbb{G}$, and the assignment of the intrinsic group, form functors between appropriate categories. Morphisms of locally compact quantum groups can be described by Hopf
$\mathbb{G}$, and the assignment of the intrinsic group, form functors between appropriate categories. Morphisms of locally compact quantum groups can be described by Hopf  $*$-homomorphisms between universal
$*$-homomorphisms between universal 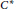 ${{C}^{*}}$-algebras, by bicharacters, or by special sorts of coactions. We show that the whole theory of completely bounded multipliers can be lifted to the universal
${{C}^{*}}$-algebras, by bicharacters, or by special sorts of coactions. We show that the whole theory of completely bounded multipliers can be lifted to the universal 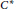 ${{C}^{*}}$-algebra level, and that the different pictures of both multipliers (reduced, universal, and as centralisers) and morphisms then interact in extremely natural ways. The intrinsic group of a quantum group can be realised as a class of multipliers, and so our techniques immediately apply. We also show how to think of the intrinsic group using the universal
${{C}^{*}}$-algebra level, and that the different pictures of both multipliers (reduced, universal, and as centralisers) and morphisms then interact in extremely natural ways. The intrinsic group of a quantum group can be realised as a class of multipliers, and so our techniques immediately apply. We also show how to think of the intrinsic group using the universal 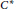 ${{C}^{*}}$-algebra picture, and then, again, how the differing views on the intrinsic group interact naturally with morphisms. We show that the intrinsic group is the “maximal classical” quantum subgroup of a locally compact quantum group, that it is even closed in the strong Vaes sense, and that the intrinsic group functor is an adjoint to the inclusion functor from locally compact groups to quantum groups.
${{C}^{*}}$-algebra picture, and then, again, how the differing views on the intrinsic group interact naturally with morphisms. We show that the intrinsic group is the “maximal classical” quantum subgroup of a locally compact quantum group, that it is even closed in the strong Vaes sense, and that the intrinsic group functor is an adjoint to the inclusion functor from locally compact groups to quantum groups.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
- 5
- Cited by




