Research Article
Convex lattice polygons of minimum area
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-367
-
- Article
-
- You have access
- Export citation
On the semigroup of an ordinary multiple point
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-6
-
- Article
-
- You have access
- Export citation
Geometric coverings of groups and their directions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-184
-
- Article
-
- You have access
- Export citation
Analyticity and quasi-Banach valued functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 369-382
-
- Article
-
- You have access
- Export citation
Function spaces and the Mosco topology
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 7-19
-
- Article
-
- You have access
- Export citation
A natural proof of the cyclotomic identity
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 185-189
-
- Article
-
- You have access
- Export citation
Iterative solution of nonlinear equations of the monotone type in Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 21-31
-
- Article
-
- You have access
- Export citation
Sums of deficiencies of algebroid functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 191-200
-
- Article
-
- You have access
- Export citation
Hermite-Fejér type interpolation and Korovkin's theorem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 383-390
-
- Article
-
- You have access
- Export citation
The differentiability of convex functions on topological linear spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 201-213
-
- Article
-
- You have access
- Export citation
On variation of equicontinuity in dynamical systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 391-397
-
- Article
-
- You have access
- Export citation
Radial growth and boundedness for Bloch functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 33-39
-
- Article
-
- You have access
- Export citation
On local equivalence for vector field systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 215-229
-
- Article
-
- You have access
- Export citation
Maximal coplanar sets of intersection points
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 41-56
-
- Article
-
- You have access
- Export citation
On a general nonlinear variational inequality
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 399-406
-
- Article
-
- You have access
- Export citation
On the isometry of surfaces preserving the lines of curvature
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 231-245
-
- Article
-
- You have access
- Export citation
A distance for similarity classes of submanifolds of a Euclidean space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 407-415
-
- Article
-
- You have access
- Export citation
On equational theories of semilattices with operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 57-70
-
- Article
-
- You have access
- Export citation
Linear functionals on some weighted Bergman spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 417-425
-
- Article
-
- You have access
- Export citation
The duality between flow charts and circuits
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 71-79
-
- Article
-
- You have access
- Export citation

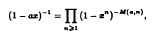
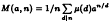 and
and 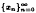 iteratively by
iteratively by 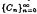 is a real sequence satisfying appropriate conditions. Then, for any given
is a real sequence satisfying appropriate conditions. Then, for any given 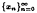 converges strongly to a solution of
converges strongly to a solution of 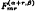 and special values of α, β it was proved by the first author in recent papers that one has uniform convergence on the whole interval [−1,1]. The second author could show by introducing the concept of asymptotic positivity how to get the known convergence results for the classical Hermite-Fejér interpolation operators. In the present paper we show, using a slightly modified Bohman-Korovkin theorem for asymptotically positive functionals, that the Hermite-Fejér type interpolation polynomials
and special values of α, β it was proved by the first author in recent papers that one has uniform convergence on the whole interval [−1,1]. The second author could show by introducing the concept of asymptotic positivity how to get the known convergence results for the classical Hermite-Fejér interpolation operators. In the present paper we show, using a slightly modified Bohman-Korovkin theorem for asymptotically positive functionals, that the Hermite-Fejér type interpolation polynomials 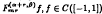 , converge pointwise to
, converge pointwise to 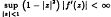 . We establish sufficient conditions for the boundedness of functions
. We establish sufficient conditions for the boundedness of functions  , then
, then