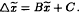Research Article
Closed linear maps from a barrelled normed space into itself need not be continuous
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-179
-
- Article
-
- You have access
- Export citation
Isomorphisms of Cayley digraphs of Abelian groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 181-188
-
- Article
-
- You have access
- Export citation
On a diophantine equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 189-198
-
- Article
-
- You have access
- Export citation
On the size of integer solutions of elliptic equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 199-206
-
- Article
-
- You have access
- Export citation
Functional means and harmonic functional means
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 207-220
-
- Article
-
- You have access
- Export citation
A closed simplicial model category for proper homotopy and shape theories
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 221-242
-
- Article
-
- You have access
- Export citation
Permutation polynomials with exponents in an arithmetic progression
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 243-252
-
- Article
-
- You have access
- Export citation
Sharp gradient estimates for eigenfunctions on Riemannian manifolds
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 253-259
-
- Article
-
- You have access
- Export citation
Class numbers of real quadratic fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 261-274
-
- Article
-
- You have access
- Export citation
Convergence of a quadrature formula for variable-signed weight functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 275-288
-
- Article
-
- You have access
- Export citation
An isodiametric problem with lattice-point constraints
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 289-294
-
- Article
-
- You have access
- Export citation
Spherical submanifolds with special quadric representations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 295-303
-
- Article
-
- You have access
- Export citation
The exponential stability of the problem of transmission of the wave equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 305-327
-
- Article
-
- You have access
- Export citation
The Weyl calculus and Clifford analysis
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 329-341
-
- Article
-
- You have access
- Export citation
On a question of Gross concerning uniqueness of entire functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 343-349
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Several classes of single variable polynomials over finite fields
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 351
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 57 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 57 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

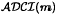 of Abelian groups. First we reduce the problem of determining Abelian
of Abelian groups. First we reduce the problem of determining Abelian 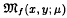 and the harmonic functional mean
and the harmonic functional mean 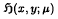 of
of 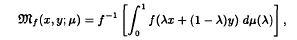
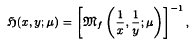
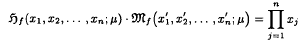
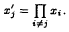
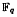 , of characteristic
, of characteristic 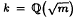 be a real quadratic field. It is well known that if 3 divides the class number of
be a real quadratic field. It is well known that if 3 divides the class number of 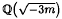 , and thus it divides
, and thus it divides 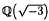 respectively. In general, the main conjecture of Iwasawa theory implies that if an odd prime
respectively. In general, the main conjecture of Iwasawa theory implies that if an odd prime 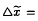
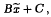 where
where 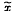 is the quadric representation of the submanifold, and
is the quadric representation of the submanifold, and