Research Article
ON SUM OF PRODUCTS AND THE ERDŐS DISTANCE PROBLEM OVER FINITE FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 21 June 2011, pp. 1-9
-
- Article
-
- You have access
- Export citation
ORDER EMBEDDING OF A MATRIX ORDERED SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 21 June 2011, pp. 10-18
-
- Article
-
- You have access
- Export citation
LANDAU’S THEOREM AND MARDEN CONSTANT FOR HARMONIC ν-BLOCH MAPPINGS
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2011, pp. 19-32
-
- Article
-
- You have access
- Export citation
ON MINIMAL SURFACES SATISFYING THE OMORI–YAU PRINCIPLE
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2011, pp. 33-39
-
- Article
-
- You have access
- Export citation
DENSE SETS OF INTEGERS WITH A PRESCRIBED REPRESENTATION FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2011, pp. 40-43
-
- Article
-
- You have access
- Export citation
POINTWISE CONVERGENCE AND SEMIGROUPS ACTING ON VECTOR-VALUED FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2011, pp. 44-48
-
- Article
-
- You have access
- Export citation
Corrigendum
LINEAR RELATIONS ON HEREDITARILY INDECOMPOSABLE NORMED SPACES – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 10 June 2011, pp. 49-52
-
- Article
-
- You have access
- Export citation
Research Article
THE QUASILINEARITY OF SOME FUNCTIONALS ASSOCIATED WITH THE RIEMANN–STIELTJES INTEGRAL
- Part of:
-
- Published online by Cambridge University Press:
- 05 April 2011, pp. 53-66
-
- Article
-
- You have access
- Export citation
ON HARMONIC BLOCH SPACES IN THE UNIT BALL OF ℂn
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2011, pp. 67-78
-
- Article
-
- You have access
- Export citation
TETRAVALENT ARC-TRANSITIVE GRAPHS WITH UNBOUNDED VERTEX-STABILIZERS
- Part of:
-
- Published online by Cambridge University Press:
- 15 March 2011, pp. 79-89
-
- Article
-
- You have access
- Export citation
ON KRULL–SCHMIDT FINITELY ACCESSIBLE CATEGORIES
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2011, pp. 90-97
-
- Article
-
- You have access
- Export citation
AN ELEMENTARY PROOF OF JAMES’ CHARACTERIZATION OF WEAK COMPACTNESS
- Part of:
-
- Published online by Cambridge University Press:
- 03 June 2011, pp. 98-102
-
- Article
-
- You have access
- Export citation
EXOTIC LEFT-ORDERINGS OF THE FREE GROUPS FROM THE DEHORNOY ORDERING
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2011, pp. 103-110
-
- Article
-
- You have access
- Export citation
ON α-LIKE RADICALS
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2011, pp. 111-115
-
- Article
-
- You have access
- Export citation
COHERENT STATES IN BERNOULLI NOISE FUNCTIONALS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2011, pp. 116-126
-
- Article
-
- You have access
- Export citation
A NOTE ON NIELSEN EQUIVALENCE IN FINITELY GENERATED ABELIAN GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2011, pp. 127-136
-
- Article
-
- You have access
- Export citation
BI-MAGIC AND OTHER GENERALIZATIONS OF SUPER EDGE-MAGIC LABELINGS
- Part of:
-
- Published online by Cambridge University Press:
- 15 June 2011, pp. 137-152
-
- Article
-
- You have access
- Export citation
ON A CURIOUS PROPERTY OF BELL NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 14 June 2011, pp. 153-158
-
- Article
-
- You have access
- Export citation
ON VERBAL SUBGROUPS IN RESIDUALLY FINITE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2011, pp. 159-170
-
- Article
-
- You have access
- Export citation
A NOTE ON EDGE-CONNECTIVITY OF THE CARTESIAN PRODUCT OF GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 06 June 2011, pp. 171-176
-
- Article
-
- You have access
- Export citation


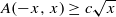 for infinitely many positive integers
for infinitely many positive integers