Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Keady, G.
1990.
The persistence of logconcavity for positive solutions of the one dimensional heat equation.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 48,
Issue. 2,
p.
246.
Dragomir, Sever S.
and
Keady, Grant
2000.
A Hadamard-jensen inequality and an application to the elastic torsion problem.
Applicable Analysis,
Vol. 75,
Issue. 3-4,
p.
285.
Hamel, François
Nadirashvili, Nikolai
and
Sire, Yannick
2020.
2018 MATRIX Annals.
Vol. 3,
Issue. ,
p.
249.
Steinerberger, Stefan
2022.
On Concavity of Solutions of the Nonlinear Poisson Equation.
Archive for Rational Mechanics and Analysis,
Vol. 244,
Issue. 2,
p.
209.
Chau, Albert
and
Weinkove, Ben
2023.
Concavity of solutions to semilinear equations in dimension two.
Bulletin of the London Mathematical Society,
Vol. 55,
Issue. 2,
p.
706.




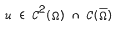 be a solution, positive in Ω, of
be a solution, positive in Ω, of