Article contents
NORMAL BASES FOR MODULAR FUNCTION FIELDS
Published online by Cambridge University Press: 02 March 2017
Abstract
We provide a concrete example of a normal basis for a finite Galois extension which is not abelian. More precisely, let 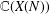 $\mathbb{C}(X(N))$ be the field of meromorphic functions on the modular curve
$\mathbb{C}(X(N))$ be the field of meromorphic functions on the modular curve 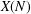 $X(N)$ of level
$X(N)$ of level 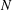 $N$. We construct a completely free element in the extension
$N$. We construct a completely free element in the extension 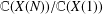 $\mathbb{C}(X(N))/\mathbb{C}(X(1))$ by means of Siegel functions.
$\mathbb{C}(X(N))/\mathbb{C}(X(1))$ by means of Siegel functions.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2017 Australian Mathematical Publishing Association Inc.
Footnotes
The second author was supported by Hankuk University of Foreign Studies Research Fund of 2016.
References
- 1
- Cited by


