Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-26T23:16:04.824Z Has data issue: false hasContentIssue false
  • English
  • Français

DEEP 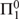${\rm{\Pi }}_1^0 $ CLASSES

Published online by Cambridge University Press:  05 July 2016

LAURENT BIENVENU  and
CHRISTOPHER P. PORTER
LAURENT BIENVENU
Affiliation:
LABORATOIRE CNRS J.-V. PONCELET 119002, BOLSHOY VLASYEVSKIY PEREULOK 11 MOSCOW, RUSSIAE-mail: laurent.bienvenu@computability.fr
CHRISTOPHER P. PORTER
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF FLORIDA GAINESVILLE, FLORIDA 32611- 8105, USAE-mail: cp@cpporter.com
Get access Rights & Permissions [Opens in a new window]

Abstract

A set of infinite binary sequences ${\cal C} \subseteq 2$ℕ is negligible if there is no partial probabilistic algorithm that produces an element of this set with positive probability. The study of negligibility is of particular interest in the context of 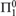${\rm{\Pi }}_1^0 $ classes. In this paper, we introduce the notion of depth for 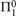${\rm{\Pi }}_1^0 $ classes, which is a stronger form of negligibility. 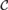Whereas a negligible ${\rm{\Pi }}_1^0 $ class ${\cal C}$ has the property that one cannot probabilistically compute a member of 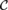${\cal C}$ with positive probability, a deep 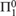${\rm{\Pi }}_1^0 $ class 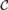${\cal C}$ has the property that one cannot probabilistically compute an initial segment of a member of 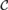${\cal C}$ with high probability. That is, the probability of computing a length n initial segment of a deep 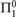${\rm{\Pi }}_1^0 $ class converges to 0 effectively in n.

We prove a number of basic results about depth, negligibility, and a variant of negligibility that we call tt-negligibility. We provide a number of examples of deep 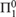${\rm{\Pi }}_1^0 $ classes that occur naturally in computability theory and algorithmic randomness. We also study deep classes in the context of mass problems, examine the relationship between deep classes and certain lowness notions in algorithmic randomness, and establish a relationship between members of deep classes and the amount of mutual information with Chaitin’s Ω.

Keywords

03D3268Q3003D80computability theoryalgorithmic randomnessΠ01.classesprobabilistic computation
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 22 , Issue 2 , June 2016 , pp. 249 - 286
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bennett, Charles H., Logical depth and physical complexity, The Universal Turing Machine: A Half-century Survey, Springer, New York, 1995, pp. 207–235.Google Scholar
Bienvenu, Laurent, Hölzl, Rupert, Porter, Christopher P., and Shafer, Paul, Randomness and semi-measures, Notre Dame Journal of Formal Logic, preprint, arXiv:1310.5133, 2014.Google Scholar
Bienvenu, Laurent and Miller, Joseph S., Randomness and lowness notions via open covers. Annals of Pure and Applied Logic, vol. 163 (2012), no. 5, pp. 506–518.Google Scholar
Bienvenu, Laurent and Porter, Christopher P., Strong reductions in effective randomness. Theoretical Computer Science, vol. 459 (2012), pp. 55–68.Google Scholar
Day, Adam and Miller, Joseph S., Density, forcing, and the covering problem, Mathematical Research Letters, vol. 22 (2015), no. 3, submitted.Google Scholar
de Leeuw, Karel, Moore, Edward F., Shannon, Claude, and Shapiro, Norman, Computability by probabilistic machines, Automata Studies, Princeton University Press, Princeton, NJ, 1956.Google Scholar
Downey, Rodney, Greenberg, Noam, and Miller, Joseph S., The upward closure of a perfect thin class. Annals of Pure and Applied Logic, vol. 156 (2008), pp. 51–58.Google Scholar
Downey, Rodney and Hirschfeldt, Denis, Algorithmic Randomness and Complexity, Theory and Applications of Computability, Springer, New York, 2010.Google Scholar
Durand, Bruno, Levin, Leonid, and Shen, Alexander, Complex tilings. The Journal of Symbolic Logic, vol. 73 (2008), no. 2, pp. 593–613.Google Scholar
Franklin, Johanna N.Y. and Ng, Keng Meng, Difference randomness. Proceedings of the American Mathematical Society, vol. 139 (2011), pp. 345–360.Google Scholar
Gács, Peter, Lecture notes on descriptional complexity and randomness, manuscript, available at http://www.cs.bu.edu/fac/gacs/recent-publ.html.Google Scholar
Gács, Peter, Exact expressions for some randomness tests, Zeitschrift fur Mathematische Logik und Grundlagen der Mathematik, vol. 26 (1980), pp. 385–394.Google Scholar
Greenberg, Noam and Miller, Joseph S., Lowness for Kurtz randomness, this Journal, vol. 74 (2009), no. 2, pp. 665–678.Google Scholar
Greenberg, Noam and Miller, Joseph S., Diagonally non-recursive functions and effective Hausdorff dimension. Bulletin of the London Mathematical Society, vol. 43 (2011), no. 4, pp. 636–654.Google Scholar
Greenberg, Noam, Miller, Joseph S., and Nies, André, PA-completeness and its weakenings, in preparation.Google Scholar
Hölzl, Rupert and Merkle, Wolfgang, Traceable sets, IFIP TCS, IFIP Advances in Information and Communication Technology, no. 323, Springer, Springer Berlin Heidelberg, 2010, pp. 301–315.Google Scholar
Jockusch, Carl and Soare, Robert, ${\rm{\Pi }}_1^0 $classes and degrees of theories. Transaction of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
Kautz, Steven M., Degrees of Random Sequences, Ph.D. Thesis, Cornell University, 1991.Google Scholar
Khan, Mushfeq, Shift-complex sequences, this Bulletin, vol. 19 (2013), no. 2, pp. 199–215.Google Scholar
Kurtz, Stuart, Randomness and genericity in the degrees of unsolvability, Ph. D dissertation, University of Illinois at Urbana, 1981.Google Scholar
Levin, Leonid A., Randomness conservation inequalities; information and independence in mathematical theories. Information and Control, vol. 61 (1984), no. 1, pp. 15–37.Google Scholar
Levin, Leonid A., Forbidden information. Journal of the ACM, vol. 60 (2013), no. 2, p. 9.Google Scholar
Levin, Leonid A. and V’yugin, Vladimir V., Invariant properties of informational bulks, Lecture Notes in Computer Science, vol. 53 (1977), pp. 359–364.Google Scholar
Levin, Leonid A. and Zvonkin, Alexander K., The complexity of finite objects and the basing of the concepts of information and randomness on the theory of algorithms. Uspekhi Matematicheskikh Nauk, vol. 25 (1970), no. 6(156), pp. 85–127.Google Scholar
Nies, André, Computability and Randomness, Oxford Logic Guides, vol. 51, Oxford University Press, Oxford, 2009.Google Scholar
Nies, André, Stephan, Frank, and Terwijn, Sebastiaan A., Randomness, relativization and Turing degrees. The Journal of Symbolic Logic, vol. 70 (2005), no. 2, pp. 515–535.Google Scholar
Rumyantsev, Andrey Yu., Everywhere complex sequences and the probabilistic method, STACS, LIPIcs, vol. 9, 2011, pp. 464–471.Google Scholar
Sacks, Gerald, Degrees of Unsolvability, Princeton University Press, Princeton, NJ, 1963.Google Scholar
Simpson, Stephen G., Mass problems and randomness, this Bulletin, vol. 11 (2005), pp. 1–27.Google Scholar
Simpson, Stephen G., An extension of the recursively enumerable Turing degrees. Journal of the London Mathematical Society, vol. 75 (2006), p. 2007.Google Scholar
Simpson, Stephen G., Mass problems associated with effectively closed sets. Tohoku Mathematical Journal, vol. 63 (2011), pp. 489–517.Google Scholar
Stephan, Frank, Martin-Löf random and PA-complete sets, Proceedings of ASL Logic Colloquium 2002, ASL Lecture Notes in Logic, vol. 27, 2006, pp. 342–348.Google Scholar
V’yugin, Vladimir V., Algebra of invariant properties of binary sequences. Problemy Peredachi Informatsii, vol. 18 (1982), no. 2, pp. 83–100.Google Scholar