Other
Dietrich Stoyan: A Tribute on the Occasion of his Seventieth Birthday
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. i-iv
-
- Article
-
- You have access
- Export citation
Stochastic Geometry and Statistical Applications
Intrinsic volumes of inscribed random polytopes in smooth convex bodies
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 605-619
-
- Article
-
- You have access
- Export citation
On the peeling procedure applied to a Poisson point process
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 620-630
-
- Article
-
- You have access
- Export citation
Criticality of the exponential rate of decay for the largest nearest-neighbor link in random geometric graphs
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 631-658
-
- Article
-
- You have access
- Export citation
Limit theorems for random spatial drainage networks
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 659-688
-
- Article
-
- You have access
- Export citation
General Applied Probability
An optimal portfolio problem in a defaultable market
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 689-705
-
- Article
-
- You have access
- Export citation
Extreme value theory, Poisson-Dirichlet distributions, and first passage percolation on random networks
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 706-738
-
- Article
-
- You have access
- Export citation
Selecting the last consecutive record in a record process
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 739-760
-
- Article
-
- You have access
- Export citation
Fluid limit theorems for stochastic hybrid systems with application to neuron models
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 761-794
-
- Article
-
- You have access
- Export citation
On optimal allocation of a continuous resource using an iterative approach and total positivity
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 795-815
-
- Article
-
- You have access
- Export citation
A fluid limit for a cache algorithm with general request processes
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 816-833
-
- Article
-
- You have access
- Export citation
Interacting branching processes and linear file-sharing networks
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 834-854
-
- Article
-
- You have access
- Export citation
On the structure and representations of max-stable processes
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 855-877
-
- Article
-
- You have access
- Export citation
A general comparison theorem for backward stochastic differential equations
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 878-898
-
- Article
-
- You have access
- Export citation
A self-regulating and patch subdivided population
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 899-912
-
- Article
-
- You have access
- Export citation
Front matter
APR volume 42 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
APR volume 42 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

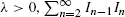 is Poisson distributed with mean λ. In this paper, we want to find an optimal stopping time τ
is Poisson distributed with mean λ. In this paper, we want to find an optimal stopping time τ