Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-26T04:25:01.021Z Has data issue: false hasContentIssue false
  • English
  • Français

SINR percolation for Cox point processes with random powers

Part of: Special processes Stochastic processes Operations research and management science Equilibrium statistical mechanics

Published online by Cambridge University Press:  23 March 2022

Benedikt Jahnel  and
András Tóbiás
Benedikt Jahnel*
Affiliation:
Weierstrass Institute for Applied Analysis and Stochastics
András Tóbiás*
Affiliation:
Technical University of Berlin
*
*Postal address: Weierstrass Institute for Applied Analysis and Stochastics, Mohrenstraße 39, 10117 Berlin, Germany. Email address: Jahnel@wias-berlin.de
**Postal address: Technical University of Berlin, Institute of Mathematics, Straße des 17. Juni 136, 10623 Berlin, Germany. Email address: Tobias@math.tu-berlin.de
Get access Rights & Permissions [Opens in a new window]

Abstract

Signal-to-interference-plus-noise ratio (SINR) percolation is an infinite-range dependent variant of continuum percolation modeling connections in a telecommunication network. Unlike in earlier works, in the present paper the transmitted signal powers of the devices of the network are assumed random, independent and identically distributed, and possibly unbounded. Additionally, we assume that the devices form a stationary Cox point process, i.e., a Poisson point process with stationary random intensity measure, in two or more dimensions. We present the following main results. First, under suitable moment conditions on the signal powers and the intensity measure, there is percolation in the SINR graph given that the device density is high and interferences are sufficiently reduced, but not vanishing. Second, if the interference cancellation factor 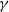$\gamma$ and the SINR threshold $\tau$ satisfy 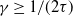$\gamma \geq 1/(2\tau)$ , then there is no percolation for any intensity parameter. Third, in the case of a Poisson point process with constant powers, for any intensity parameter that is supercritical for the underlying Gilbert graph, the SINR graph also percolates with some small but positive interference cancellation factor.

Keywords

Signal-to-interference ratioCox point processPoisson point processcontinuum percolationSINR percolationGilbert graphBoolean modelstabilizationrandom powerdegree bound

MSC classification

Primary: 82B43: Percolation 60G55: Point processes 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 90B18: Communication networks
Type
Original Article
Information
Advances in Applied Probability , Volume 54 , Issue 1 , March 2022 , pp. 227 - 253
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlberg, D., Tassion, V. and Teixeira, A. (2018). Sharpness of the phase transition for continuum percolation in $\Bbb R^2$ . Prob. Theory Relat. Fields 172, 525–581.10.1007/s00440-017-0815-8CrossRefGoogle Scholar
Blaszczyszyn, B. and Yogeshwaran, D. (2013). Clustering and percolation of point processes. Electron. J. Prob. 18, 1–20.10.1214/EJP.v18-2468CrossRefGoogle Scholar
Bollobás, B. and Riordan, O. (2006). Percolation. Cambridge University Press.10.1017/CBO9781139167383CrossRefGoogle Scholar
Coupier, D., Dereudre, D. and Le Stum, S. (2020). Absence of percolation for Poisson outdegree-one graphs. Ann. Inst. H. Poincaré Prob. Statist. 56, 1179–1202.10.1214/19-AIHP998CrossRefGoogle Scholar
Cali, E. et al. (2018). Percolation for D2D networks on street systems. Proc. 16th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt 2018), Institute of Electrical and Electronics Engineers, Piscataway, NJ, pp. 1–6.10.23919/WIOPT.2018.8362866CrossRefGoogle Scholar
Chiu, S., Stoyan, D., Kendall, W. and Mecke, J. (2013). Stochastic Geometry and Its Applications. John Wiley, New York.10.1002/9781118658222CrossRefGoogle Scholar
Daley, D. J. (1971). The definition of a multi-dimensional generalization of shot noise. J. Appl. Prob. 8, 128–135.10.2307/3211843CrossRefGoogle Scholar
Dousse, O., Baccelli, F. and Thiran, P. (2005). Impact of interferences on connectivity in ad hoc networks. IEEE/ACM Trans. Networking 1, 425–436.10.1109/TNET.2005.845546CrossRefGoogle Scholar
Dousse, O. et al. (2006). Percolation in the signal to interference ratio graph. J. Appl. Prob. 43, 552–562.10.1239/jap/1152413741CrossRefGoogle Scholar
Franceschetti, M. and Meester, R. (2007). Random Networks for Communication—From Statistical Physics to Information Systems. Cambridge University Press.Google Scholar
Gilbert, E. N. (1961). Random plane networks. J. SIAM 9, 533–543.Google Scholar
Gouéré, J.-B. (2008). Subcritical regimes in the Poisson Boolean model of continuum percolation. Ann. Prob. 36, 1209–1220.10.1214/07-AOP352CrossRefGoogle Scholar
Gouéré, J.-B. (2009). Subcritical regimes in some models of continuum percolation. Ann. Appl. Prob. 19, 1292–1318.10.1214/08-AAP575CrossRefGoogle Scholar
Gouéré, J.-B. and Théret, M. (2018). Equivalence of some subcritical properties in continuum percolation. Bernoulli 25, 3714–3733.Google Scholar
Grimmett, G. (1999). Percolation, 2nd edn. Springer, Berlin.10.1007/978-3-662-03981-6CrossRefGoogle Scholar
Hirsch, C., Jahnel, B. and Cali, E. (2019). Continuum percolation for Cox point processes. Stoch. Process. Appl. 129, 3941–3966.10.1016/j.spa.2018.11.002CrossRefGoogle Scholar
Jahnel, B. and Tóbiás, A. (2020). Exponential moments for planar tessellations. J. Statist. Phys. 179, 90–109.10.1007/s10955-020-02521-3CrossRefGoogle Scholar
Jahnel, B., Tóbiás, A. and Ca, li, E. (2021). Phase transitions for the Boolean model of continuum percolation for Cox point processes.  To appear in Brazilian J. Prob. Statist.Google Scholar
Jahnel, B. and Tóbiás, A. (2021). SINR percolation for Cox point processes with random powers. (Extended online version of the present paper.) Available at https://arxiv.org/abs/1912.07895.Google Scholar
Kingman, J. F. C. (1993). Poisson Processes. Oxford University Press, New York.Google Scholar
Kong, Z. and Yeh, E. M. (2007). Directed percolation in wireless networks with interference and noise. Preprint. Available at https://arxiv.org/abs/0712.2469.Google Scholar
Löffler, R. (2019). Percolation phase transitions for the SIR model with random powers. Masters Thesis, Technical University of Berlin Institute of Mathematics. Available at https://arxiv.org/abs/1908.07375.Google Scholar
Liggett, T. M., Schonmann, R. H. and Stacey, A. M. (1997). Domination by product measures. Ann. Prob. 25, 71–95.10.1214/aop/1024404279CrossRefGoogle Scholar
Matheron, G. (1975). Random Sets and Integral Geometry. John Wiley, New York.Google Scholar
Meester, R. and Roy, R. (1996). Continuum Percolation. Cambridge University Press.10.1017/CBO9780511895357CrossRefGoogle Scholar
Penrose, M. and Pisztora, á. (1996). Large deviations for discrete and continuous percolation. Adv. Appl. Prob. 28, 29–52.10.2307/1427912CrossRefGoogle Scholar
Tóbiás, A. (2019). Message routeing and percolation in interference limited multihop networks. Doctoral Thesis, Technical University of Berlin Institute of Mathematics. Available at https://depositonce.tu-berlin.de/handle/11303/9293.Google Scholar
Tóbiás, A. (2020). Signal to interference ratio percolation for Cox point processes. Latin Amer. J. Prob. Math. Statist. 17, 273–308.10.30757/ALEA.v17-11CrossRefGoogle Scholar