Article contents
The sharp threshold for jigsaw percolation in random graphs
Published online by Cambridge University Press: 07 August 2019
Abstract
We analyse the jigsaw percolation process, which may be seen as a measure of whether two graphs on the same vertex set are ‘jointly connected’. Bollobás, Riordan, Slivken, and Smith (2017) proved that, when the two graphs are independent binomial random graphs, whether the jigsaw process percolates undergoes a phase transition when the product of the two probabilities is 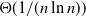 $\Theta({1}/{(n\ln n)})$. We show that this threshold is sharp, and that it lies at
$\Theta({1}/{(n\ln n)})$. We show that this threshold is sharp, and that it lies at 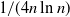 ${1}/{(4n\ln n)}$.
${1}/{(4n\ln n)}$.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © Applied Probability Trust 2019
References
- 1
- Cited by




