Article contents
Set Reconstruction by Voronoi Cells
Published online by Cambridge University Press: 04 January 2016
Abstract
For a Borel set A and a homogeneous Poisson point process η in 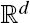 of intensity λ>0, define the Poisson–Voronoi approximation Aη of A as a union of all Voronoi cells with nuclei from η lying in A. If A has a finite volume and perimeter, we find an exact asymptotic of E Vol(AΔ Aη) as λ→∞, where Vol is the Lebesgue measure. Estimates for all moments of Vol(Aη) and Vol(AΔ Aη) together with their asymptotics for large λ are obtained as well.
of intensity λ>0, define the Poisson–Voronoi approximation Aη of A as a union of all Voronoi cells with nuclei from η lying in A. If A has a finite volume and perimeter, we find an exact asymptotic of E Vol(AΔ Aη) as λ→∞, where Vol is the Lebesgue measure. Estimates for all moments of Vol(Aη) and Vol(AΔ Aη) together with their asymptotics for large λ are obtained as well.
MSC classification
- Type
- Stochastic Geometry and Statistical Applications
- Information
- Copyright
- © Applied Probability Trust
Footnotes
Partially supported by RFBR (10-01-00242), NSh-4472.2010.1, RFBR-DFG (09-0191331), and DFG (436 RUS 113/962/0-1 R) grants.
References
- 7
- Cited by




