Hostname: page-component-848d4c4894-xfwgj Total loading time: 0 Render date: 2024-06-21T16:52:28.597Z Has data issue: false hasContentIssue false
  • English
  • Français

Seneta constants for the supercritical Bellman–Harris process

Published online by Cambridge University Press:  01 July 2016

H.-J. Schuh
H.-J. Schuh*
Affiliation:
University of Melbourne
*
∗Present address: Johannes Gutenberg-Universität in Mainz, Fachbereich 17, Mathematik, Saarstr. 21, Postfach 3980, D-6500 Mainz, W. Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

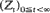Let be a supercritical Bellman-Harris process with finite offspring mean. Cohn [17] has shown that there always exist constants Ct such that limt→∞Zt/Ct = W almost surely for some non-degenerate random variable W. In this paper we give an alternative proof, based on the study of (Zt) as a point process. Our methods are to some extent analytical and parallel Seneta's [18] and Heyde's [11] approaches in the case of the Galton–Watson process. We further identify Ct as 1/(–log Ft(–1)(γ)), where Ft(γ) = E(γzt), i.e. the norming constants found by Seneta [18] for the Galton–Watson process, apply also to the Bellman-Harris process. Finally we derive a weak law of large numbers for W, prove that W is continuous on (0,∞) and show that W has [0,∞) as its support.

Keywords

AGE-DEPENDENT BRANCHING PROCESSNORMING CONSTANTSMULTITYPE BRANCHING PROCESSPOINT PROCESSGENERAL BRANCHING PROCESSAGE DISTRIBUTIONMALTHUSIAN PARAMETERSEQUENCE OF BACKWARD ITERATESHEYDE-TYPE MARTINGALEASSOCIATED GENERATION PROCESSWEAK LAW OF LARGE NUMBERSCONTINUITY AND POSITIVITY OF THE DISTRIBUTION OF W
Type
Research Article
Information
Advances in Applied Probability , Volume 14 , Issue 4 , December 1982 , pp. 732 - 751
Copyright
Copyright © Applied Probability Trust 1982 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Athreya, K. B. (1969) On the supercritical age-dependent branching process. Ann Math. Statist. 40, 743–763.Google Scholar
[2] Athreya, K. B. and Kaplan, N. (1976) Convergence of the age distribution in the one-dimensional supercritical age-dependent branching process. Ann. Prob. 4, 38–50.Google Scholar
[3] Athreya, K. B. and Kaplan, N. (1978) Additive property and its applications in branching processes. In Branching Processes ed. Joffe, A. and Ney, P. E., 27–60.Google Scholar
[4] Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer-Verlag, Berlin.Google Scholar
[5] Biggins, J. D. and Grey, D. R. (1979) Continuity of limit random variables in the branching random walk. J. Appl. Prob. 16, 740–749.Google Scholar
[6] Breiman, L. (1968) Probability. Addision-Wesley, Reading, Ma.Google Scholar
[7] Cohn, H. (1982) Norming constants for the finite mean supercritical Bellman-Harris process. Z. Wahrscheinlichkeitsth. CrossRefGoogle Scholar
[8] Cohn, H. and Schuh, H.-J. (1980) On the continuity and the positivity of the finite part of the limit distribution of an irregular branching process with infinite mean. J. Appl. Prob. 17, 696–703.Google Scholar
[9] Feller, W. (1971) An Introduction to Probability and its Applications. Vol. II, 2nd edn. Wiley, New York.Google Scholar
[10] Harris, T. E. (1963) The Theory of Branching Processes. Springer-Verlag, Berlin.Google Scholar
[11] Heyde, C. C. (1970) Extension of a result by Seneta for the supercritical branching process. Ann. Math. Statist. 41, 739–742.CrossRefGoogle Scholar
[12] Hoppe, F. M. (1976) Supercritical multitype branching processes. Ann. Prob. 4, 393–401.Google Scholar
[13] Jagers, P. (1969) Renewal theory and the a.s. convergence of branching processes. Ark. Mat. 7, 495–504.CrossRefGoogle Scholar
[14] Kuczek, T. (1982) On the convergence of the empiric age distribution for one dimensional supercritical age-dependent branching processes. Ann. Prob. Google Scholar
[15] Kuczek, T. (1980) On Some Results in Branching Processes and GA/G/8 Queues with Applications to Biology. , Purdue University.Google Scholar
[16] Nerman, O. (1979) On the Convergence of Supercritical General Branching Process. , University of Goteborg.Google Scholar
[17] Schuh, H.-J. and Barbour, A. D. (1977) On the asymptotic behaviour of branching processses with infinite mean. Adv. Appl. Prob. 9, 681–723.Google Scholar
[18] Seneta, E. (1968) On recent theorems concerning the supercritical Galton-Watson process. Ann. Math. Statist. 39, 2098–2102.Google Scholar
[19] Seneta, E. (1975) Characterization by functional equations of branching process limit laws. In Statistical Distributions in Scientific Work, Vol. 3, ed. Patil, G. P. et al, Reidel, Dordrecht, 249–254.Google Scholar