Article contents
Random Symmetrizations of Convex Bodies
Published online by Cambridge University Press: 22 February 2016
Abstract
In this paper we investigate the asymptotic behavior of sequences of successive Steiner and Minkowski symmetrizations. We state an equivalence result between the convergences of those sequences for Minkowski and Steiner symmetrizations. Moreover, in the case of independent (and not necessarily identically distributed) directions, we prove the almost-sure convergence of successive symmetrizations at exponential rate for Minkowski, and at rate 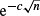 with c > 0 for Steiner.
with c > 0 for Steiner.
MSC classification
- Type
- Stochastic Geometry and Statistical Applications
- Information
- Copyright
- © Applied Probability Trust
References
- 6
- Cited by




