Hostname: page-component-76fb5796d-5g6vh Total loading time: 0 Render date: 2024-04-25T18:09:48.831Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal control of service rates in networks of queues

Published online by Cambridge University Press:  01 July 2016

Richard R. Weber  and
Shaler Stidham Jr
Richard R. Weber*
Affiliation:
University of Cambridge
Shaler Stidham Jr*
Affiliation:
University of North Carolina
*
∗Postal address: Queens’ College, Cambridge, CB3 9ET, UK.
∗∗ Postal address: Department of Operations Research and Systems Analysis, University of North Carolina, Chapel Hill, NC 27514, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a monotonicity result for the problem of optimal service rate control in certain queueing networks. Consider, as an illustrative example, a number of ·/M/1 queues which are arranged in a cycle with some number of customers moving around the cycle. A holding cost hi(xi) is charged for each unit of time that queue i contains xi customers, with hi being convex. As a function of the queue lengths the service rate at each queue i is to be chosen in the interval 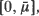, where cost ci(μ) is charged for each unit of time that the service rate μis in effect at queue i. It is shown that the policy which minimizes the expected total discounted cost has a monotone structure: namely, that by moving one customer from queue i to the following queue, the optimal service rate in queue i is not increased and the optimal service rates elsewhere are not decreased. We prove a similar result for problems of optimal arrival rate and service rate control in general queueing networks. The results are extended to an average-cost measure, and an example is included to show that in general the assumption of convex holding costs may not be relaxed. A further example shows that the optimal policy may not be monotone unless the choice of possible service rates at each queue includes 0.

Keywords

CONTROL OF QUEUESCYCLES OF QUEUESDYNAMIC PROGRAMMINGMONOTONE POLICIESSERIES OF QUEUES
Type
Research Article
Information
Advances in Applied Probability , Volume 19 , Issue 1 , March 1987 , pp. 202 - 218
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of this author was partially supported by the U.S. Army Research Office, Contract DAAG29-82-k-0152, at North Carolina State University, Raleigh, NC, USA, and by the Science and Engineering Research Council, at the University of Cambridge, UK.

References

Bertsekas, D. (1976) Dynamic Programming and Stochastic Control. Academic Press, New York.Google Scholar
Crabill, T. (1972) Optimal control of a service facility with variable exponential service time and constant animal rate. Management Sci. 18, 560–566.CrossRefGoogle Scholar
Crabill, T., Gross, D., and Magazine, M. (1977) A classified bibliography of research on optimal design and control of queues. Operat. Res. 25, 219–232.CrossRefGoogle Scholar
Davis, E. (1977) Optimal Control of Arrivals to a Two-Server Queueing System with Separate Queues. Ph.D. Dissertation, Program in Operations Research, North Carolina State University, Raleigh.Google Scholar
Ephremides, A., Varaiya, P., and Walrand, J. (1980) A simple dynamic routing problem. IEEE Trans. Autom. Control 25, 690–693.CrossRefGoogle Scholar
Ghoneim, H. (1980) Optimal Control of Arrivals to a Network of Two Queues in Series. Ph.D dissertation, Program in Operations Research, North Carolina State University, Raleigh.Google Scholar
Hajek, B. (1984) Optimal control of two interacting service stations. IEEE Trans. Autom. Control 29, 491–499.CrossRefGoogle Scholar
Hordijk, A. and Van Der Duyn Schouten, F. A. (1983) Average optimal policies in Markov decision drift processes with applications to a queueing and replacement model. Adv. Appl. Prob. 15, 274–303.CrossRefGoogle Scholar
Johansen, S. and Stidham, S. (1980) Control of arrivals to a stochastic input output system. Adv. Appl. Prob. 12, 972–999.CrossRefGoogle Scholar
Jo, K. Y. and Stidham, S. (1983) Optimal service-rate control of M/G/1 queueing systems using phase methods. Adv. Appl. Prob. 15, 616–637.CrossRefGoogle Scholar
Lippman, S. (1975) Applying a new device in the optimization of exponential queueing systems. Operat. Res. 23, 687–710.CrossRefGoogle Scholar
Lippman, S. and Stidham, S. (1977) Individual versus social optimization in exponential congestion systems. Operat. Res. 25, 233–247.CrossRefGoogle Scholar
Lu, F. V. and Sefozo, R. F. (1984) M/M/1 queueing decision processes with monotone hysteritic optimal policies. Operat. Res. 32, 1116–1132.CrossRefGoogle Scholar
Rosberg, Z., Varaiya, P., and Walrand, J. (1982) Optimal control of service in tandem queues. IEEE Trans. Autom. Control 27, 600–610.CrossRefGoogle Scholar
Ross, S. (1970) Applied Probability Models with Optimization Applications. Holden-Day, San Francisco.Google Scholar
Schal, M. (1977) On negative dynamic programming with irreducible Markov chains and the average cost criterion. Bonner Math. Schr. 98, 93–97.Google Scholar
Serfozo, R. (1979) An equivalence between discrete and continuous time Markov decision processes. Operat. Res. 27, 616–620.CrossRefGoogle Scholar
Serfozo, R. F. (1981) Optimal control of random walks, birth and death processes, and queues. Adv. Appl. Prob. 13, 61–83.CrossRefGoogle Scholar
Sobel, M. (1974) Optimal operation of queues. In Mathematical Methods in Queueing Theory, ed. Clarke, A. B., Springer-Verlag, Berlin, 231–261.CrossRefGoogle Scholar
Stidham, S. (1985) Optimal control of admission to a queueing system. IEEE Trans. Autom. Control. To appear.CrossRefGoogle Scholar
Stidham, S. and Prabhu, N. (1974) Optimal control of queueing systems. In Mathematical Methods in Queueing Theory, ed. Clarke, A. B., Springer-Verlag, Berlin, 263–294.CrossRefGoogle Scholar
Stidham, S. and Weber, R. (1987) Monotonic and insensitive optimal policies for control of arrival and service rates in queues. Operat. Res. To appear.Google Scholar
Topkis, D. (1978) Minimizing a submodular function on a lattice. Operat. Res. 26, 305–321.CrossRefGoogle Scholar
Weber, R. (1978) On the optimal assignment of customers to parallel servers. J. Appl. Prob. 15, 406–413.CrossRefGoogle Scholar
Whittle, P. (1983) Optimization over Time. Wiley, Chichester.Google Scholar
Winston, W. (1977) Optimality of the shortest line discipline. J. Appl. Prob. 14, 181–189.CrossRefGoogle Scholar