Consider the following migration process based on a closed network of N queues with 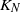$K_N$ customers. Each station is a $\cdot$/M/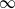$\infty$ queue with service (or migration) rate 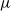$\mu$. Upon departure, a customer is routed independently and uniformly at random to another station. In addition to migration, these customers are subject to a susceptible–infected–susceptible (SIS) dynamics. That is, customers are in one of two states: I for infected, or S for susceptible. Customers can swap their state either from I to S or from S to I only in stations. More precisely, at any station, each susceptible customer becomes infected with the instantaneous rate 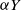$\alpha Y$ if there are Y infected customers in the station, whereas each infected customer recovers and becomes susceptible with rate 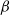$\beta$. We let N tend to infinity and assume that 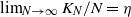$\lim_{N\to \infty} K_N/N= \eta $, where 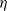$\eta$ is a positive constant representing the customer density. The main problem of interest concerns the set of parameters of such a system for which there exists a stationary regime where the epidemic survives in the limiting system. The latter limit will be referred to as the thermodynamic limit. We use coupling and stochastic monotonicity arguments to establish key properties of the associated Markov processes, which in turn allow us to give the structure of the phase transition diagram of this thermodynamic limit with respect to 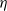$\eta$. The analysis of the Kolmogorov equations of this SIS model reduces to that of a wave-type PDE for which we have found no explicit solution. This plain SIS model is one among several companion stochastic processes that exhibit both random migration and contagion. Two of them are discussed in the present paper as they provide variants to the plain SIS model as well as some bounds and approximations. These two variants are the departure-on-change-of-state (DOCS) model and the averaged-infection-rate (AIR) model, which both admit closed-form solutions. The AIR system is a classical mean-field model where the infection mechanism based on the actual population of infected customers is replaced by a mechanism based on some empirical average of the number of infected customers in all stations. The latter admits a product-form solution. DOCS features accelerated migration in that each change of SIS state implies an immediate departure. This model leads to another wave-type PDE that admits a closed-form solution. In this text, the main focus is on the closed stochastic networks and their limits. The open systems consisting of a single station with Poisson input are instrumental in the analysis of the thermodynamic limits and are also of independent interest. This class of SIS dynamics has incarnations in virtually all queueing networks of the literature.