Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-07-07T21:32:12.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Fcfs infinite bipartite matching of servers and customers

Part of: Operations research and management science Computer system organization Markov processes

Published online by Cambridge University Press:  01 July 2016

René Caldentey ,
Edward H. Kaplan  and
Gideon Weiss
René Caldentey*
Affiliation:
New York University
Edward H. Kaplan*
Affiliation:
Yale School of Management, Yale School of Medicine, and Yale School of Engineering and Applied Science
Gideon Weiss*
Affiliation:
University of Haifa
*
∗ Postal address: IOMS Department, Stern Business School, New York University, New York. Email address: rcaldent@stern.nyu.edu
∗∗ Postal address: Yale School of Management, Box 208200, New Haven, CT 06520-8200, USA. Email address: edward.kaplan@yale.edu
∗∗∗ Postal address: Department of Statistics, The University of Haifa, Mount Carmel 31905, Israel. Email address: gweiss@stat.haifa.ac.il
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

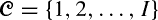We consider an infinite sequence of customers of types and an infinite sequence of servers of types 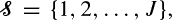where a server of type j can serve a subset of customer types C(j) and where a customer of type i can be served by a subset of server types S(i). We assume that the types of customers and servers in the infinite sequences are random, independent, and identically distributed, and that customers and servers are matched according to their order in the sequence, on a first-come–first-served (FCFS) basis. We investigate this process of infinite bipartite matching. In particular, we are interested in the rate ri,j that customers of type i are assigned to servers of type j. We present a countable state Markov chain to describe this process, and for some previously unsolved instances, we prove ergodicity and existence of limiting rates, and calculate ri,j.

Keywords

Service systemsfirst-come–first-servedinfinite bipartite matchingMarkov chain

MSC classification

Primary: 90B22: Queues and service
Secondary: 60J20: Applications of Markov chains and discrete-time Markov processes on general state spaces (social mobility, learning theory, industrial processes, etc.) 68M20: Performance evaluation; queueing; scheduling
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 41 , Issue 3 , September 2009 , pp. 695 - 730
Copyright
Copyright © Applied Probability Trust 2009 

References

Adan, I., Foley, R. D. and McDonald, D. R. (2007). Exact asymptotics of the stationary distribution of a Markov chain: a production model. EURANDOM Report 2008-036, Eindhoven, Netherlands. Available at http://www.eurandom.nl/EURANDOMreports.htm.Google Scholar
Aksin, Z., Armony, M. and Mehrotra, V. (2007). The modern call-center: a multi-disciplinary perspective on operations management research. Production Operat. Manag. 16, 665–688.Google Scholar
Brémaud, P. (1999). Markov Chains. Springer, New York.Google Scholar
Birch, M. W. (1963). Maximum likelihood in three-way contingency tables. J. R. Statist. Soc. B 25, 220–233.Google Scholar
Bishop, Y. M. M. and Fienberg, S. E. (1969). Incomplete two-dimensional contingency tables. Biometrics 25, 119–128.Google Scholar
Caldentey, R. A. and Kaplan, E. H. (2002). A heavy traffic approximation for queues with restricted customer-service matchings. Unpublished manuscript.Google Scholar
Dao-Thi, T.-H. and Mairesse, J. (2006). Zero-automatic networks. In Proc. VALUETOOLS (Pisa, Italy), ACM, New York.Google Scholar
Dao-Thi, T.-H. and Mairesse, J. (2007). Zero-automatic queues and product form. Adv. Appl. Prob. 39, 502–536.Google Scholar
Durrett, R. (1995). Probability: Theory and Examples, 2nd edn. Duxbury Press, Belmont, CA.Google Scholar
Fayolle, G., Malyshev, V. A. and Menshikov, M. V. (1995). Topics in the Constructive Theory of Countable Markov Chains. Cambridge University Press.Google Scholar
Fienberg, S. E. (1970). Quasi-independence and maximum likelihood estimation in incomplete contingency tables. J Amer. Statist. Assoc. 65, 1610–1615.CrossRefGoogle Scholar
Ford, L. R. Jr. and Fulkerson, D. R. (1962). Flows in Networks. Princeton University Press.Google Scholar
Garnett, O. and Mandelbaum, A. (2000). An introduction to skill-based routing and its operational complexities. Unpublished manuscript. Available at http://iew3.technion.ac.il/serveng/Lectures/SBR.pdf.Google Scholar
Goodman, L. (1968). The analysis of cross classified data: independence, quasi-independence, and interactions in contingency tables with and without missing entries. J. Amer. Statist. Assoc. 63, 1091–1131.Google Scholar
Hwang, N. H. C. (1981). Fundamentals of Hydraulic Engineering Systems. Prentice Hall, Englewood Cliffs, NJ.Google Scholar
Kaplan, E. H. (1984). Managing the demand for public housing. ORC Tech. Rep. 183, MIT.Google Scholar
Kaplan, E. H. (1988). A public housing queue with reneging and task-specific servers. Decision Sci. 19, 383–391.Google Scholar
Mairesse, J. (2005). Random walks on groups and monoids with a Markovian harmonic measure. Electron. J. Prob. 10, 1417–1441.Google Scholar
Mairesse, J. and Mathéus, F. (2007). Random walks on free products of cyclic groups. J. London Math. Soc. 75, 47–66. Appendix available at http://arxiv.org/abs/math/0509208.Google Scholar
Talreja, R. and Whitt, W. (2007). Fluid models for overloaded multiclass many-service queueing systems with FCFS routeing. Manag. Sci. 54, 1513–1527.Google Scholar
Zenios, S. A. (1999). Modeling the transplant waiting list: a queueing model with reneging. Queueing Systems 31, 239–251.Google Scholar