Hostname: page-component-848d4c4894-sjtt6 Total loading time: 0 Render date: 2024-06-24T18:55:11.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Bootstrap percolation in inhomogeneous random graphs

Part of: Graph theory Special processes

Published online by Cambridge University Press:  07 August 2023

Hamed Amini Open the ORCID record for Hamed Amini [Opens in a new window] ,
Nikolaos Fountoulakis Open the ORCID record for Nikolaos Fountoulakis [Opens in a new window]  and
Konstantinos Panagiotou
Hamed Amini*
Affiliation:
University of Florida
Nikolaos Fountoulakis*
Affiliation:
University of Birmingham
Konstantinos Panagiotou*
Affiliation:
University of Munich
*
*Postal address: Department of Industrial and Systems Engineering, University of Florida, 468 Weil Hall, Gainesville, FL 32611, USA. Email address: aminil@ufl.edu
**Postal address: School of Mathematics, University of Birmingham, Birmingham B15 2TT, UK. Email address: n.fountoulakis@bham.ac.uk
***Postal address: Mathematical Institute, University of Munich, Theresienstr. 39, 80333 München, Germany. Email address: kpanagio@math.lmu.de
Get access Rights & Permissions [Opens in a new window]

Abstract

A bootstrap percolation process on a graph with n vertices is an ‘infection’ process evolving in rounds. Let 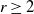$r \ge 2$ be fixed. Initially, there is a subset of infected vertices. In each subsequent round, every uninfected vertex that has at least r infected neighbors becomes infected as well and remains so forever.

We consider this process in the case where the underlying graph is an inhomogeneous random graph whose kernel is of rank one. Assuming that initially every vertex is infected independently with probability 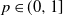$p \in (0,1]$, we provide a law of large numbers for the size of the set of vertices that are infected by the end of the process. Moreover, we investigate the case 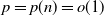$p = p(n) = o(1)$, and we focus on the important case of inhomogeneous random graphs exhibiting a power-law degree distribution with exponent 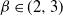$\beta \in (2,3)$. The first two authors have shown in this setting the existence of a critical 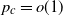$p_c =o(1)$ such that, with high probability, if 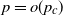$p =o(p_c)$, then the process does not evolve at all, whereas if 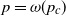$p = \omega(p_c)$, then the final set of infected vertices has size 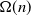$\Omega(n)$. In this work we determine the asymptotic fraction of vertices that will eventually be infected and show that it also satisfies a law of large numbers.

Keywords

Bootstrap percolationrandom graphssharp threshold

MSC classification

Primary: 05C80: Random graphs
Secondary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
Original Article
Information
Advances in Applied Probability , Volume 56 , Issue 1 , March 2024 , pp. 156 - 204
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, J. and Lev, U. (2003). Bootstrap percolation: visualizations and applications. Brazilian J. Phys. 33, 641–644.CrossRefGoogle Scholar
Albert, R. and Barabási, A. (2002). Statistical mechanics of complex networks. Rev. Modern Phys. 74, 47–97.CrossRefGoogle Scholar
Amini, H. (2010). Bootstrap percolation and diffusion in random graphs with given vertex degrees. Electron. J. Combinatorics 17, article no. R25.CrossRefGoogle Scholar
Amini, H. (2010). Bootstrap percolation in living neural networks. J. Statist. Phys. 141, 459–475.CrossRefGoogle Scholar
Amini, H., Cont, R. and Minca, A. (2016). Resilience to contagion in financial networks. Math. Finance 26, 329–365.CrossRefGoogle Scholar
Amini, H. and Fountoulakis, N. (2014). Bootstrap percolation in power-law random graphs. J. Statist. Phys. 155, 72–92.CrossRefGoogle Scholar
Amini, H. and Minca, A. (2016). Inhomogeneous financial networks and contagious links. Operat. Res. 64, 1109–1120.CrossRefGoogle Scholar
Athreya, K. and Ney, P. (1972). Branching Processes. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
Balogh, J. and Bollobás, B. (2006). Bootstrap percolation on the hypercube. Prob. Theory Relat. Fields 134, 624–648.CrossRefGoogle Scholar
Balogh, J., Bollobás, B., Duminil-Copin, H. and Morris, R. (2012). The sharp threshold for bootstrap percolation in all dimensions. Trans. Amer. Math. Soc. 36, 2667–2701.CrossRefGoogle Scholar
Balogh, J., Bollobás, B. and Morris, R. (2009). Bootstrap percolation in three dimensions. Ann. Prob. 37, 1329–1380.CrossRefGoogle Scholar
Balogh, J., Peres, Y. and Pete, G. (2006). Bootstrap percolation on infinite trees and non-amenable groups. Combinatorics Prob. Comput. 15, 715–730.CrossRefGoogle Scholar
Balogh, J. and Pittel, B. G. (2007). Bootstrap percolation on the random regular graph. Random Structures Algorithms 30, 257–286.CrossRefGoogle Scholar
Bollobás, B., Janson, S. and Riordan, O. (2007). The phase transition in inhomogeneous random graphs. Random Structures Algorithms 31, 3–122.CrossRefGoogle Scholar
Cerf, R. and Manzo, F. (2002). The threshold regime of finite volume bootstrap percolation. Stoch. Process. Appl. 101, 69–82.CrossRefGoogle Scholar
Chalupa, J., Leath, P. L. and Reich, G. R. (1979). Bootstrap percolation on a Bethe lattice. J. Phys. C 12, L31–L35.CrossRefGoogle Scholar
Chung, F. and Lu, L. (2002). Connected components in random graphs with given expected degree sequences. Ann. Combinatorics 6, 125–145.CrossRefGoogle Scholar
Chung, F. and Lu, L. (2003). The average distance in a random graph with given expected degrees. Internet Math. 1, 91–113.CrossRefGoogle Scholar
Chung, F., Lu, L. and Vu, V. (2004). The spectra of random graphs with given expected degrees. Internet Math. 1, 257–275.CrossRefGoogle Scholar
Detering, N., Meyer-Brandis, T. and Panagiotou, K. (2019). Bootstrap percolation in directed inhomogeneous random graphs. Electron. J. Combinatorics 26, article no. P3.12.Google Scholar
Detering, N., Meyer-Brandis, T., Panagiotou, K. and Ritter, D. (2019). Managing default contagion in inhomogeneous financial networks. SIAM J. Financial Math. 10, 578–614.CrossRefGoogle Scholar
Fontes, L. and Schonmann, R. (2008). Bootstrap percolation on homogeneous trees has 2 phase transitions. J. Statist. Phys. 132, 839–861.CrossRefGoogle Scholar
Fontes, L. R., Schonmann, R. H. and Sidoravicius, V. (2002). Stretched exponential fixation in stochastic Ising models at zero temperature. Commun. Math. Phys. 228, 495–518.CrossRefGoogle Scholar
Holroyd, A. E. (2003). Sharp metastability threshold for two-dimensional bootstrap percolation. Prob. Theory Relat. Fields 125, 195–224.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000). Random Graphs. John Wiley, New York.CrossRefGoogle Scholar
Janson, S., Łuczak, T., Turova, T. and Vallier, T. (2012). Bootstrap percolation on the random graph ${G}_{n,p}$ . Ann. Appl. Prob. 22, 1989–2047.CrossRefGoogle Scholar
Lotka, A. J. (1926). The frequency distribution of scientific productivity. J. Washington Acad. Sci. 16, 317–323.Google Scholar
Mitzenmacher, M. (2004). A brief history of generative models for power law and lognormal distributions. Internet Math. 1, 226–251.CrossRefGoogle Scholar
Morris, R. (2009). Zero-temperature Glauber dynamics on $\mathbb{Z}^d$ . Prob. Theory Relat. Fields 149, 417–434.CrossRefGoogle Scholar
Pareto, V. (1896). Cours d’Économie Politique. Dronz, Geneva.Google Scholar
Sabhapandit, S., Dhar, D. and Shukla, P. (2002). Hysteresis in the random-field Ising model and bootstrap percolation. Phys. Rev. Lett. 88, article no. 197202.CrossRefGoogle ScholarPubMed
Sausset, F., Toninelli, C., Biroli, G. and Tarjus, G. (2010). Bootstrap percolation and kinetically constrained models on hyperbolic lattices. J. Statist. Phys. 138, 411–430.CrossRefGoogle Scholar
Söderberg, B. (2002). General formalism for inhomogeneous random graphs. Phys. Rev. E 66, article no. 066121.CrossRefGoogle ScholarPubMed
Tlusty, T. and Eckmann, J. (2009). Remarks on bootstrap percolation in metric networks. J. Phys. A 42, article no. 205004.CrossRefGoogle Scholar
Toninelli, C., Biroli, G. and Fisher, D. S. (2006). Jamming percolation and glass transitions in lattice models. Phys. Rev. Lett. 96, article no. 035702.CrossRefGoogle ScholarPubMed
Torrisi, G., Garetto, M. and Leonardi, E. (2018). Bootstrap percolation on the stochastic block model. Preprint. Available at https://arxiv.org/abs/1812.09107.Google Scholar
Van der Hofstad, R. (2016). Random Graphs and Complex Networks, Vol. 1. Cambridge University Press.CrossRefGoogle Scholar
Wormald, N. (1999). The differential equation method for random graph processes and greedy algorithms. In Lectures on Approximation and Randomized Algorithms, eds M. Karonski and H.-J. Prömel, Polish Scientific Publishers PWN, pp. 73–155.Google Scholar
Wormald, N. C. (1995). Differential equations for random processes and random graphs. Ann. Appl. Prob. 5, 1217–1235.CrossRefGoogle Scholar