Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-19T23:07:36.944Z Has data issue: false hasContentIssue false
  • English
  • Français

An unusual stochastic order relation with some applications in sampling and epidemic theory

Part of: Combinatorial probability Distribution theory - Probability Special processes

Published online by Cambridge University Press:  01 July 2016

Claude Lefevre  and
Philippe Picard
Claude Lefevre*
Affiliation:
Université Libre de Bruxelles
Philippe Picard*
Affiliation:
Université de Lyon 1
*
∗Postal address: Institut de Statistique, C.P. 210, Université Libre de Bruxelles, Boulevard du Triomphe, B-1050 Bruxelles, Belgique.
∗∗Postal address: Mathématiques Appliquées, Université de Lyon 1, 43 Boulevard du 11 Novembre 1918, F-69622 Villeurbanne Cedex, France.
Get access Rights & Permissions [Opens in a new window]

Abstract

One expects, intuitively, that the total damage caused by an epidemic increases, in a certain sense, with the infection intensity exerted by the infectives during their lifelength. The original object of the present work is to make precise in which probabilistic terms such a statement does indeed hold true, when the spread of the disease is described by a collective Reed–Frost model and the global cost is represented by the final size and severity. Surprisingly, this problem leads us to introduce an order relation for 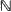-valued random variables, unusual in the literature, based on the descending factorial moments. Further applications of the ordering occur when comparing certain sampling procedures through the number of un-sampled individuals. In particular, it is used to reinforce slightly comparison results obtained earlier for two such samplings.

Keywords

FINAL SIZE AND SEVERITYFAMILY OF POLYNOMIALSFACTORIAL MOMENTSCOMPARTMENTAL URN MODELDEATH PROCESS

MSC classification

Primary: 60C05: Combinatorial probability
Secondary: 60E15: Inequalities; stochastic orderings 60K99: None of the above, but in this section
Type
Research Article
Information
Advances in Applied Probability , Volume 25 , Issue 1 , March 1993 , pp. 63 - 81
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bailey, N. T. J. (1975) The Mathematical Theory of Infectious Diseases and its Applications. Griffin, London.Google Scholar
Ball, F. and Donnelly, P. (1987) Interparticle correlation in death processes with application to variability in compartmental models. Adv. Appl. Prob. 19, 755–766.CrossRefGoogle Scholar
Bernard, S. R. (1977) An urn model study of variability within a compartment. Bull. Math. Biol. 39, 463–470.CrossRefGoogle Scholar
Daley, D. J. (1990) The size of epidemics with variable infectious periods. Submitted for publication.Google Scholar
Donnelly, P. and Whitt, W. (1989) On reinforcement–depletion compartmental urn models. J. Appl. Prob. 26, 477–489.CrossRefGoogle Scholar
Klefsjö, B. (1983) A useful ageing property based on the Laplace transform. J. Appl. Prob. 20, 615–626.Google Scholar
Lefevre, Cl. and Picard, Ph. (1989) On the formulation of discrete-time epidemic models. Math. Biosci. 95, 27–35.Google Scholar
Lefevre, Cl. (1990) Stochastic epidemic models for S.I.R. infectious diseases: a brief survey of the recent general theory. In Stochastic Processes in Epidemic Theory, ed. Gabriel, J. P., Lefèvre, CL. and Picard, Ph., Lecture Notes in Biomathematics 86, pp. 1–12, Springer-Verlag, New York.Google Scholar
Lefevre, Cl. and Michaletzky, G. (1990) Interparticle dependence in a linear death process subjected to a random environment. J. Appl. Prob. 27, 491–498.Google Scholar
Lefevre, Cl. and Picard, Ph. (1990) A non-standard family of polynomials and the final size distribution of Reed–Frost epidemic processes. Adv. Appl. Prob. 22, 25–48.CrossRefGoogle Scholar
Lefevre, Cl. and Picard, Ph. (1992) A multivariate stochastic ordering by the mixed descending factorial moments with applications. In Stochastic Inequalities, ed. Shaked, M. and Tong, Y. L., pp. 235–252, IMS Lecture Notes Series.Google Scholar
Malice, M. P. and Kryscio, R. J. (1989) On the role of variable incubation periods in simple epidemic models. I.M.A. J. Math. Appl. Med. Biol. 6, 233–242.Google Scholar
Malice, M. P. and Lefevre, Cl. (1988) On some effects of variability in the Weiss epidemic model. Commun. Stat.-Theory Methods 17, 3723–3731.CrossRefGoogle Scholar
Martin-Löf, A. (1986) Symmetric sampling procedures, general epidemic processes and their threshold limit theorems. J. Appl. Prob. 23, 265–282.Google Scholar
Picard, Ph. and Lefevre, Cl. (1990) A unified analysis of the final size and severity distribution in collective Reed–Frost epidemic processes. Adv. Appl. Prob. 22, 269–294.Google Scholar
Ross, S. M. (1983) Stochastic Processes. Wiley, New York.Google Scholar
Shenton, L. R. (1981) A reinforcement–depletion urn problem. I. Basic theory. Bull. Math. Biol. 43, 327–340.Google Scholar
Stoyan, D. (1983) Comparison Methods for Queues and Other Stochastic Models. Wiley, New York.Google Scholar