Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-07-07T18:50:11.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Well-timed diffusion approximations

Published online by Cambridge University Press:  01 July 2016

John B. Walsh
John B. Walsh*
Affiliation:
The University of British Columbia
*
∗Postal address: Department of Mathematics. The University of British Columbia, #121–1984 Mathematics Road, University Campus, Vancouver, B.C., Canada V6T 1Y4.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X be a Markov process on the line. Under certain conditions it is possible to find a diffusion process 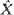which is an approximation to X in the following sense:

(1) X can be embedded in 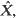that is there are stopping times (Tt) such that {Xt, t ≥ 0} and 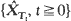have the same distribution;

(2) for each t, E{Tt} = t.

We call 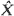the well-timed diffusion approximation to X, and suggest that it is useful for approximating quantities like the first-exit probabilities and expected first-exit times of X.

We determine the well-timed approximation in several special cases and give an asymptotic approximation for use in cases in which 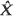cannot be exactly determined.

Keywords

DIFFUSION APPROXIMATIONTIME-CHANGEMARTINGALE EMBEDDINGS
Type
Research Article
Information
Advances in Applied Probability , Volume 13 , Issue 2 , June 1981 , pp. 352 - 368
Copyright
Copyright © Applied Probability Trust 1981 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Baxter, J. R. and Chacon, R. V. (1974) Potentials of stopped distributions. Illinois J. Math. 18, 649–656.CrossRefGoogle Scholar
[2] Breiman, L. (1968) Probability. Addison-Wesley, Reading, MA.Google Scholar
[3] Chacon, R. V. and Walsh, J. B. (1976) One-dimensional potential embedding. In Séminaire de Probabilités X. Lecture Notes in Mathematics 511, Springer-Verlag, Berlin.Google Scholar
[4] Dinges, H. (1974) Stopping sequences. In Séminaire de Probabilités VIII. Lecture Notes in Mathematics 381, Springer-Verlag, Berlin.Google Scholar
[5] Doob, J. L. (1953) Stochastic Processes. Wiley, New York.Google Scholar
[6] Dubins, L. E. (1968) On a theorem of Skorokhod. Ann. Math. Statist. 39, 2094–2097.CrossRefGoogle Scholar
[7] Dubins, L. E. and Schwartz, G. (1968) On continuous martingales. Proc. Nat. Acad. Sci. U.S.A. 53, 913–916.CrossRefGoogle Scholar
[8] Heath, D. (1974) Skorokhod stopping via potential theory. In Séminaire de Probabilités VIII. Lecture Notes in Mathematics 381, Springer-Verlag, Berlin.Google Scholar
[9] McKean, H. P. (1969) Stochastic Integrals. Academic Press, London.Google Scholar
[10] Monroe, I. (1972) On embedding right-continuous martingales in Brownian motion. Ann. Math. Statist. 43, 1293–1311.Google Scholar
[11] Root, D. H. (1969) The existence of certain stopping times on Brownian motion. Ann. Math. Statist. 40, 715–718.CrossRefGoogle Scholar
[12] Skorokhod, A. V. (1965) Studies in the Theory of Random Processes. Addison-Wesley, Reading, MA.Google Scholar