Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Boshuizen, Frans A.
and
Kertz, Robert P.
1999.
Smallest-fit selection of random sizes under a sum constraint: weak convergence and moment comparisons.
Advances in Applied Probability,
Vol. 31,
Issue. 1,
p.
178.
Gnedin, Alexander V.
1999.
Sequential selection of an increasing subsequence from a sample of random size.
Journal of Applied Probability,
Vol. 36,
Issue. 4,
p.
1074.
Boshuizen, Frans A.
and
Kertz, Robert P.
1999.
Smallest-fit selection of random sizes under a sum constraint: weak convergence and moment comparisons.
Advances in Applied Probability,
Vol. 31,
Issue. 1,
p.
178.
Gnedin, Alexander V.
1999.
Sequential selection of an increasing subsequence from a sample of random size.
Journal of Applied Probability,
Vol. 36,
Issue. 04,
p.
1074.
Bruss, F.Thomas
and
Delbaen, Freddy
2001.
Optimal rules for the sequential selection of monotone subsequences of maximum expected length.
Stochastic Processes and their Applications,
Vol. 96,
Issue. 2,
p.
313.
Bruss, F. Thomas
and
Delbaen, Freddy
2004.
A central limit theorem for the optimal selection process for monotone subsequences of maximum expected length.
Stochastic Processes and their Applications,
Vol. 114,
Issue. 2,
p.
287.
Kaluszka, M.
Okolewski, A.
and
Szymanska, K.
2005.
Sharp bounds for L-statistics from dependent samples of random length.
Journal of Statistical Planning and Inference,
Vol. 127,
Issue. 1-2,
p.
71.
ARLOTTO, ALESSANDRO
and
STEELE, J. MICHAEL
2011.
Optimal Sequential Selection of a Unimodal Subsequence of a Random Sequence.
Combinatorics, Probability and Computing,
Vol. 20,
Issue. 6,
p.
799.
Gribonval, Rémi
Cevher, Volkan
and
Davies, Mike E.
2012.
Compressible Distributions for High-Dimensional Statistics.
IEEE Transactions on Information Theory,
Vol. 58,
Issue. 8,
p.
5016.
Cain, Nicholas
and
Shea-Brown, Eric
2013.
Impact of Correlated Neural Activity on Decision-Making Performance.
Neural Computation,
Vol. 25,
Issue. 2,
p.
289.
Tunc, Sait
Donmez, Mehmet Ali
and
Kozat, Suleyman Serdar
2013.
Optimal Investment Under Transaction Costs: A Threshold Rebalanced Portfolio Approach.
IEEE Transactions on Signal Processing,
Vol. 61,
Issue. 12,
p.
3129.
Bruss, F. Thomas
2014.
Grenzen einer jeden Gesellschaft.
Jahresbericht der Deutschen Mathematiker-Vereinigung,
Vol. 116,
Issue. 3,
p.
137.
Arlotto, Alessandro
Gans, Noah
and
Steele, J. Michael
2014.
Markov Decision Problems Where Means Bound Variances.
Operations Research,
Vol. 62,
Issue. 4,
p.
864.
KIWI, MARCOS
and
SOTO, JOSÉ A.
2015.
Longest Increasing Subsequences of Randomly Chosen Multi-Row Arrays.
Combinatorics, Probability and Computing,
Vol. 24,
Issue. 1,
p.
254.
Caballero, Javier A.
Lepora, Nathan F.
Gurney, Kevin N.
and
Chacron, Maurice J.
2015.
Probabilistic Decision Making with Spikes: From ISI Distributions to Behaviour via Information Gain.
PLOS ONE,
Vol. 10,
Issue. 4,
p.
e0124787.
Arlotto, Alessandro
Nguyen, Vinh V.
and
Steele, J. Michael
2015.
Optimal online selection of a monotone subsequence: a central limit theorem.
Stochastic Processes and their Applications,
Vol. 125,
Issue. 9,
p.
3596.
Bruss, F. Thomas
and
Duerinckx, Mitia
2015.
Resource dependent branching processes and the envelope of societies.
The Annals of Applied Probability,
Vol. 25,
Issue. 1,
Arlotto, Alessandro
Mossel, Elchanan
and
Steele, J. Michael
2016.
Quickest online selection of an increasing subsequence of specified size.
Random Structures & Algorithms,
Vol. 49,
Issue. 2,
p.
235.
Peng, Peichao
and
Steele, J.
2016.
Sequential selection of a monotone subsequence from a random permutation.
Proceedings of the American Mathematical Society,
Vol. 144,
Issue. 11,
p.
4973.
Maghsudi, Setareh
and
Hossain, Ekram
2017.
Distributed User Association in Energy Harvesting Small Cell Networks: An Exchange Economy With Uncertainty.
IEEE Transactions on Green Communications and Networking,
Vol. 1,
Issue. 3,
p.
294.
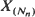 and
and 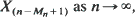 as n →∞, both for fixed s, and where s =sn is an increasing function of n.
as n →∞, both for fixed s, and where s =sn is an increasing function of n.



