Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mollison, Denis
1977.
Spatial Contact Models for Ecological and Epidemic Spread.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 39,
Issue. 3,
p.
283.
Mollison, Denis
1978.
Markovian contact processes.
Advances in Applied Probability,
Vol. 10,
Issue. 1,
p.
85.
Mollison, Denis
1978.
Markovian contact processes.
Advances in Applied Probability,
Vol. 10,
Issue. 1,
p.
85.
Sch�rger, Klaus
1979.
On the asymptotic geometrical behaviour of a class of contact interaction processes with a monotone infection rate.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 48,
Issue. 1,
p.
35.
Biggins, J. D.
1980.
Biological Growth and Spread.
Vol. 38,
Issue. ,
p.
57.
Schürger, Klaus
1980.
On the asymptotic geometrical behaviour of percolation processes.
Journal of Applied Probability,
Vol. 17,
Issue. 02,
p.
385.
Biggins, John D.
1980.
Spatial spread in branching processes.
Advances in Applied Probability,
Vol. 12,
Issue. 3,
p.
549.
Schürger, Klaus
1981.
A class of branching processes on a lattice with interactions.
Advances in Applied Probability,
Vol. 13,
Issue. 1,
p.
14.
Schürger, Klaus
1981.
A class of branching processes on a lattice with interactions.
Advances in Applied Probability,
Vol. 13,
Issue. 1,
p.
14.
Durrett, Richard
and
Griffeath, David
1982.
Contact processes in several dimensions.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 59,
Issue. 4,
p.
535.
Klebaner, C. F.
1982.
Branching random walk in varying environments.
Advances in Applied Probability,
Vol. 14,
Issue. 2,
p.
359.
Kagan, Y. Y.
1982.
Stochastic model of earthquake fault geometry.
Geophysical Journal International,
Vol. 71,
Issue. 3,
p.
659.
Durrett, Richard
1988.
Crabgrass, measles and gypsy moths: An introduction to modern probability.
Bulletin of the American Mathematical Society,
Vol. 18,
Issue. 2,
p.
117.
Neveu, J.
1988.
Seminar on Stochastic Processes, 1987.
p.
223.
Ney, Peter
1991.
Spatial Stochastic Processes.
p.
3.
Ball, Frank G.
1991.
Dynamic population epidemic models.
Mathematical Biosciences,
Vol. 107,
Issue. 2,
p.
299.
Gravner, Janko
and
Griffeath, David
1993.
Threshold growth dynamics.
Transactions of the American Mathematical Society,
Vol. 340,
Issue. 2,
p.
837.
Vatutin, V. A.
and
Zubkov, A. M.
1993.
Branching processes. II.
Journal of Soviet Mathematics,
Vol. 67,
Issue. 6,
p.
3407.
Tautu, Petre
1994.
Fractals in Biology and Medicine.
p.
86.
Isopi, Marco
and
Newman, Charles M.
1994.
Speed of parallel processing for random task graphs.
Communications on Pure and Applied Mathematics,
Vol. 47,
Issue. 3,
p.
361.
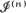 be the set of positions of the nth-generation people, scaled by the factor n–1. It is shown that when the process survives
be the set of positions of the nth-generation people, scaled by the factor n–1. It is shown that when the process survives 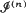 looks like a convex set
looks like a convex set 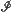 for large n. An analogous result is established for an age-dependent branching process in which people also have positions. In certain cases an explicit formula for the asymptotic shape is given.
for large n. An analogous result is established for an age-dependent branching process in which people also have positions. In certain cases an explicit formula for the asymptotic shape is given.



